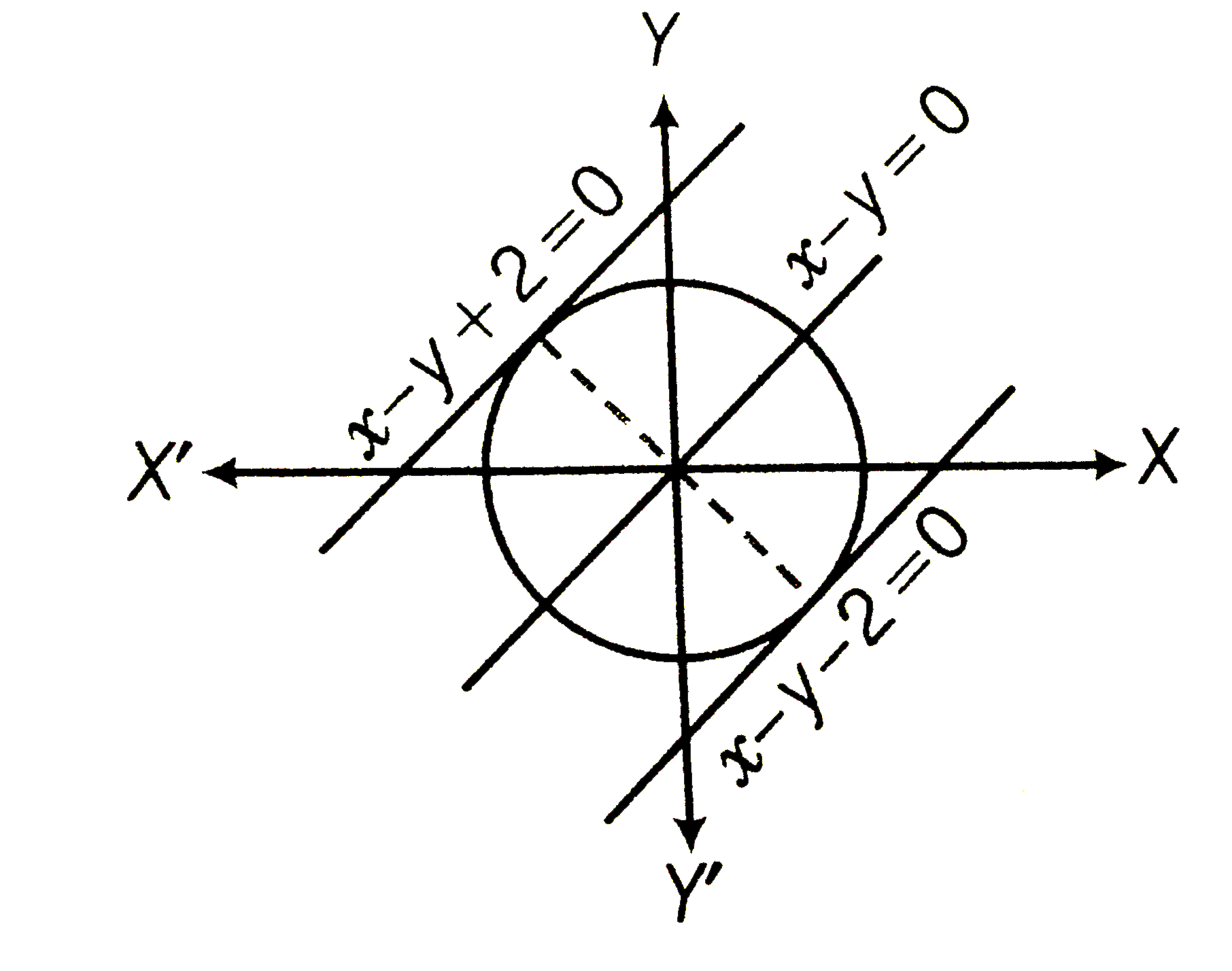
The equation of the circle having x-y-2=0 and x-y+2=0 as two langents and x-y=0 as diameter, is
x2+y2+2x−2y+1=0
x2+y22x+2y+1=0
x2+y2=2
x2+y2=1
The correct Answer is:C
Since, the equation of tangents x-y-2=0 and x-y+2=0 are parallel. ∴ distance between them= diameter of the circle =2−(2)√12+12=4√2=2√2 [∴d=c2−c1√a2+b2<br>radius =1/2(2sqrt2=sqrt2 it is clear from the that centre lies on the origin. ∴ equation of cricle is (x−0)2+(y−0)2=(√2)2 rArrx^(2)+y^(2)=2
Topper's Solved these Questions
Similar Questions
The equation of the circle having the lines x2+2xy+3x+6y=0 as its normals and having size just suffcient to contain the circle x(x−4)+y(y−3)=0 is
View SolutionThe equations of two diameters of a circle are x−2y+1=0 and x+y−2=0 and the length of the chord intercepted on the straight line 3x+4y+8=0 by the circle is 6 units. Find the equation of the circle.
View Solution
Knowledge Check
The equation of the the circle having x - y - 2 = 0 and x - y + 2 = 0 as two tangents , and x + y = 0 as a diameter is
Ax2+y2+2x−2y+1=0Bx2+y2−2x+2y−1=0Cx2+y2=2Dx2+y2=1Equation of the circle on the common chord of the circles x2+y2−ax=0andx2+y2−ay=0 as a diameter is
A2x2+2y2−ax−ay=0Bx2+y2−ax−ay=0C2x2+2y2+ax+ay=0Dx2+y2−x−y+a=0
The equation of the circle having its centre on the line x+2y−3=0 and passing through the points of intersection of the circles x2+y2−2x−4y+1=0andx2+y2−4x−2y+4=0 is
View SolutionThe equation of the circle having its centre on the line x+2y−3=0 and passing through the points of intersection of the circles x2+y2−2x−4y+1=0andx2+y2−4x−2y+4=0 is x2+y2−6x+7=0 x2+y2−3y+4=0 c.x2+y2−2x−2y+1=0 x2+y2+2x−4y+4=0
View SolutionThe equation of the circle having the center on the line x+2y−3=0 and passing through the point intersection of the circles x2+y2−2x−4y+1=0andx2+y2−4x−2y+4=0 is x2+y2−6x+7=0 x2+y2−3u−2y+4=0 x2+y2−2x−2y+1=0 x2+y2+2x−2y+4=0
View SolutionThe equation of the circle having its centre on the line x+2y−3=0 and passing through the points of intersection of the circles x2+y2−2x−4y+1=0andx2+y2−4x−2y+4=0 is x2+y2−6x+7=0 x2+y2−3y+4=0 c.x2+y2−2x−2y+1=0 x2+y2+2x−4y+4=0
View SolutionThe equation of tangent to the circle x2+y2−2x+8y−23=0 having slope 3
View SolutionThe equation of the circle having the intercept on the line y+2x=0 by the circle x2+y2+4x+6y=0 as a diameter is : (A) 5x2+5y2−8x+16y=0 (B) 5x2+5y2+8x−16y=0 (C) 5x2+5y2−8x−16y=0 (D) 5x2+5y2+8x±16y=0
View Solution