Theorem 9.3 : Two triangles having the same base (or equal bases) and equal areas lie between the same parallels.

Video Solution

Text Solution

Verified by Experts

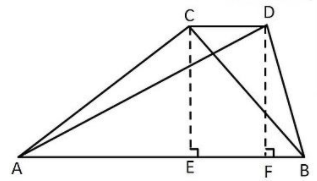
Since $C E ⊥ A B$ and $D F ⊥ A B$ Since, lines are perpendicular to same line are parallel to each other.
$C E ∣ ∣ D F$
Now,
$a r (A B C) = \frac{1}{2} \times Base \times B B' H e i g h t$
$a r (A B C) = \frac{1}{2} \times A B \times C E$
Similarly, $a r (A B D) = \frac{1}{2} \times A B \times D F$
Thus,
$a r (A B C) = a r (A B D)$
$C F = D F$
In $C D F E$
$C E ∣ ∣ D F$ and $C E = D F$
Since one pair of opposite sides is equal and parallel, $C D F E$ is parallelogram.

Updated on:21/07/2023

If P,R,T are the area of a parallelogram , a rhombus and a triangle standing on the same base and between the same parallels, which of the following is true ?
A $R \leq P \leq T$
B $P > R > T$
CR=P=T
DR=P=2T
Two parallelograms are on equal bases and between the same parallels.
The ratio of their areas is
A $1 : 2$
B $1 : 1$
C $2 : 1$
D $3 : 1$
Which of the following figures lie on the same base and between the same parallels ?
A
B
C
Dall of these