Triangles on the same base and between the same parallel are equal in area.
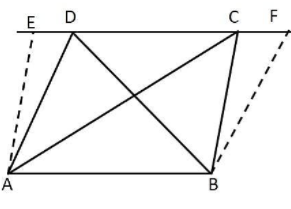
In ABFD
DF∣∣AB and BF∣∣AD
Thus, both pair of opposite sides are parallel.
Hence, ABFD id a parallelogram.
Similarly, we can prove that ABCE is a parallelogram with same base and between two parallels AB and EF.
ar(ABFD)=ar(ABCE)
In parallelogram ABFD,
Since diagonal of a parallelogram divides it into two congruent triangles.
△ABD≅△FBD
Area of congruent triangles are equal,
ar(ABD)=ar(FBD)
ar(ABFD)=2ar(ABD)
Similarly, we can prove that
ar(ABCE)=2ar(ABC)
Thus,
2ar(ABD)=2ar(ABC)
ar(ABD)=ar(ABC)
Topper's Solved these Questions
- NCERT THEOREMSBOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 9.3
1 Video
- NCERT THEOREMSBOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.1
1 Video
- NCERT THEOREMSBOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 9.1
1 Video
- LINES AND ANGLESBOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - SOLVED EXAMPLES
8 Videos
- NUMBER SYSTEMSBOOK - NCERTCHAPTER - NUMBER SYSTEMSEXERCISE - EXERCISE 1.4
2 Videos
Similar Questions
Triangles on the same base and between the same parallels are equal in area. GIVEN : Two triangles ABC and PBC on the same base BC and between the same parallel lines BC and AP. TO PROVE : ar(ABC)=ar(PBC) CONSTRUCTION : Through B, draw BDCA intersecting PA produced in D and through C, draw CQBP, intersecting line AP in Q.
View SolutionA ||gm and a rectangle on the same base and between the same parallels are equal in area
View Solution
Knowledge Check
Assertion (A) : In a trapezium ABCD, we have AB ||DC and the diagonals AC and BD intersect at O.
Then, ar(△AOD)=ar(△BOC).

Reason (R ) : Triangle on the same base between the same parallels are equal in area.ABoth Assertion (A) and Reason (R ) are true and Reason (R ) is a correct explansion of Assertion (A).BBoth Assertion (A) and Reason (R ) are true but Reason (R ) is not a correct explansion of Assertion (A).CAssertion (A) is true and Reason (R ) is false.DAssertion (A) is false and Reason (R ) is true.
Figures on the same base and between the same parallels
View SolutionParallelograms on the same base and between the same parallel are equal in area.
View SolutionTheorem 9.1 : Parallelograms on the same base and between the same parallels are equal in area.
View SolutionProve that Parallelograms on the same base and between the same parallels are equal in area.
View SolutionUsing vectors, prove that the parallelogram on the same base and between the same parallels are equal in area.
View SolutionProve by vector method that the parallelogram on the same base and between the same parallels are equal in area.
View SolutionProve that parallelograms on the same base and between the same parallels have the same area.
View Solution
