Prove that If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
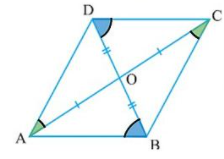
In △AOD and △COB
OA=OC (given)
∠AOD=∠COB (vertically opposite angles)
OD=OB (given)
Thus, by SAS congruency, △AOD and △COB are congruent.
Therefore, ∠OAD=∠OCB
For lines AB and CD with transversal BD,
∠ABO and ∠CDO are alternate angles and are equal.
Thus, AB∣∣CD
Similarly, we can prove that AD∣∣BC
Topper's Solved these Questions
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 8.8
Explore 1 Video
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 8.9
Explore 1 Video
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 8.6
Explore 1 Video
- LINES AND ANGLESBook:NCERTChapter:LINES AND ANGLESExercise:SOLVED EXAMPLES
Explore 8 Videos
- NUMBER SYSTEMSBook:NCERTChapter:NUMBER SYSTEMSExercise:EXERCISE 1.4
Explore 2 Videos
Similar Questions
Prove that If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
View SolutionGiven below are some pairs of statements. Combine each pair using if and only if:
(i) p: If a quadrilateral-is equiangular, then it is a rectangle.
q: If a quadrilateral is a rectangle, then it is equiangular.
(ii) p: If the sum of the digits of a number is divisible by 3, then the number is divisible by 3.
q: If a number is divisble by 3, then the sum of its digits is divisible by 3.
(iii) p: A quadrilateral is a parallelogram if its diagonals bisect each other.
q: If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
(iv) p: If f(a) = 0, then (x -a) is a factor of polynomial f(x).
q: If (x-a) is a factor of polynomial f(x), thenf(a) = 0.
(v) p: If a square matrix A is invertible, then |A| is nonzero.
q: If A is a square matrix such that |A| is nonzero, then A is invertible.
View SolutionGiven statements . Identify the statements given below as contrapositive or converse of each other.
If a quadrilateral is a parallelogram, then its diagonals bisect each other.
(i) If the diagonals of a quadrilateral do not bisect each other, then the quadrilateral is not a parallelogram.
(ii) If the diagronals of a quadrilateral bisect each other, then it is a parallelogram.
View SolutionGiven the following statements :
If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
Identify these as contrapositive or converse of each other.
View SolutionGiven statements in (a) and (b). Identify the statements given below as contrapositive or converse of each other.
(a) If you live in Delhi, then you have winter clothes.
(i) If you do not have winter clothes, then you do not live in Delhi.
(ii) If you have winter clothes, then you live in Delhi.
(b)If a quadrilateral is a parallelogram, then its diagonals bisect each other.
(i) If the diagonals of a quadrilateral do not bisect each other, then the quadrilateral is not a parallelogram.
(ii) If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
View SolutionSome statements are given in (a) and (b) identify the statements given below as contrapositive or converse of each other.
(a) if you live in Delhi,then you have winter clothes. (i) if you do not have winter clothes, then you do not live in Delhi.
(ii) if you do not have winter clothes, then you do not live in delhi.
(b) if a quadrilateral is a parallelogram, then its diagonals biset each other.
(i) if the diagonals of a quadrilateral do not biset each other, then the quadrilateral is not a parallelogram.
(ii) if the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
View SolutionGiven statements in (a) and (b) identify the statements given below as contrapositive or converse of each other.
(a) if you live in delhi , then you have winter clothes .
(i) if you do not have winter clothes, then clothes.
(ii) if you have winter clothes, then you its in delhi.
(b)if a quadrilateral is a parallelogram, then its diagonals bisect each other.
(i) if the diagonals of a quadrilateral do not bisect each other, then the quadrilateral is not a parallelogram.
(ii) if the diagonals of a quadrilateral bisect each other, then it is a paralleogram.
View SolutionProve, by vector method, that the diagonals of a parallelogram bisect each other , conversely, if the diagonals of a quadrilateral bisect each other, it is a parallelogram.
View SolutionIf the diagonals of a quadrilateral bisect each other, it is a __________.
View SolutionProve using vectors: The diagonals of a quadrilateral bisect each other iff it is a parallelogram.
View Solution

