prove that the line segment joining the mid-points of two sides of a triangle is parallel to the third side.
To prove that the line segment joining the midpoints of two sides of a triangle is parallel to the third side, we will follow these steps:
1. Draw Triangle and Identify Midpoints:
Let triangle ABC be given. Identify the midpoints D and E of sides AC and AB respectively.
2. Construct a Parallel Line:
Draw a line through point C that is parallel to line segment DE (the line joining midpoints D and E). Let this line intersect the extended line AD at point F.
3. Identify Angles:
Since DE is parallel to CF, the angles ∠ADE and ∠FCD are alternate interior angles. Therefore, we have:
∠ADE=∠FCD
4. Use Midpoint Definition:
Since D is the midpoint of AC, we have:
AD=DC
5. Identify Vertically Opposite Angles:
The angles ∠ADE and ∠CDF are vertically opposite angles. Thus, we have:
∠ADE=∠CDF
6. Establish Congruence:
Now we have two angles and one side (AD = DC) in triangle ADE and triangle CFD. By the Angle-Side-Angle (ASA) congruence criterion, we can say:
△ADE≅△CFD
7. Conclude Corresponding Parts:
From the congruence of the triangles, we can conclude:
DE=CF
and since DE is parallel to CF, we can also state that BC is equal to EF.
8. Form a Parallelogram:
Since DE is equal to CF and BC is equal to EF, quadrilateral BCEF is a parallelogram.
9. Final Conclusion:
In a parallelogram, opposite sides are parallel. Therefore, we conclude that:
DE∥BC
Thus, we have proved that the line segment joining the midpoints of two sides of a triangle is parallel to the third side.
Let triangle ABC be given. Identify the midpoints D and E of sides AC and AB respectively.
Draw a line through point C that is parallel to line segment DE (the line joining midpoints D and E). Let this line intersect the extended line AD at point F.
Since DE is parallel to CF, the angles ∠ADE and ∠FCD are alternate interior angles. Therefore, we have:
∠ADE=∠FCD
Since D is the midpoint of AC, we have:
AD=DC
The angles ∠ADE and ∠CDF are vertically opposite angles. Thus, we have:
∠ADE=∠CDF
Now we have two angles and one side (AD = DC) in triangle ADE and triangle CFD. By the Angle-Side-Angle (ASA) congruence criterion, we can say:
△ADE≅△CFD
From the congruence of the triangles, we can conclude:
DE=CF
and since DE is parallel to CF, we can also state that BC is equal to EF.
Since DE is equal to CF and BC is equal to EF, quadrilateral BCEF is a parallelogram.
In a parallelogram, opposite sides are parallel. Therefore, we conclude that:
DE∥BC
Topper's Solved these Questions
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 8.10
Explore 1 Video
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 9.1
Explore 1 Video
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 8.8
Explore 1 Video
- LINES AND ANGLESBook:NCERTChapter:LINES AND ANGLESExercise:SOLVED EXAMPLES
Explore 8 Videos
- NUMBER SYSTEMSBook:NCERTChapter:NUMBER SYSTEMSExercise:EXERCISE 1.4
Explore 2 Videos
Similar Questions
Knowledge Check
Assertion : ABCD and PQRC are rectangles and Q is a midpoint of AC. Then DP = PC.
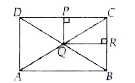
Reason : The line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of it.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.
The line joining the mid-points of two sides of a triangle is parallel to the third side.
View Solutionprove that the line segment joining the mid-points of two sides of a triangle is parallel to the third side.
View SolutionProve that the line joining the mid-points of the two sides of a triangle is parallel to the third side.
View SolutionProve that the line joining the middle points of the two sides of a triangle is parallel to the third side.
View SolutionUsing Theorem 6.2, prove that the line joining the mid-point of any two sides of a triangle is parallel to the third side. (Recall that you have done it in class IX).
View SolutionProve that the line segment joining the middle points of two sides of a triangle is half the third side.
View SolutionThe line segment joining the mid-points of any two sides of a triangle is parallel to the third side of a triangle.
View Solution

