Show that the enerty of a charged capacitor is 12CV2. Also express this in other forms.
To charge a capacitor, an external agent has to do work against the electrostatic forces due to the charges already present on the plates of the capacitor.
Let C be the capacitance of the capacitor. Let Q and V be the final charge and the potential difference respectively when the capacitor is charged. Let q be the charge on the capacitor at an intermediate stage during the charging and v, the corresponding potential difference between the plates. The work done in bringing additional small charge dp from infinity and depositing it on the capacitor is
dW = potential difference × charge = vdq
But, C=qv ∴v=qC ∴dW=qCdq
The total work done in charging the capacitor is
W=∫dW=Q∫0qdqC=1C[q22]Q0=12Q2C
Now, Q=CV ∴W=12CV2=12QV
This work is stored in the form of potential energy, in the electric field in the medium between the plates of the capacitor.
∴ Energy stored in a charged capacitor =12Q2C=12CV2=12QV
Topper's Solved these Questions
- DERIVATIONS-IIBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:DERIVATIONS-IIExercise:Current Electricity
Explore 6 Videos
- DERIVATIONS-IIBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:DERIVATIONS-IIExercise:Magnetism
Explore 1 Video
- DERIVATIONS-IIBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:DERIVATIONS-IIExercise:Interference and Diffraction
Explore 4 Videos
- DERIVATIONS-IBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:DERIVATIONS-IExercise:Assignments
Explore 9 Videos
- DISTINGUISH BETWEENBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:DISTINGUISH BETWEENExercise:Assingment
Explore 3 Videos
Similar Questions
Knowledge Check
If the potential difference across a plane parallel plate capacitor is doubled then the potential energy of the capacitor is doubled then the potential energy of the capacitor becomes four times under all conditions
The potential energy U stored in the capacitor is U=12CV2, where C and V have usual meaning.ABoth A and R falseBBoth A and R true and R is not correct reason for ACA is true and R is falseDBoth A and R are true and R is correct reason of A.A capacitor of capacitance C is connected across a battery of potential difference V. The energy stored in the capacitor is 12CV2
The energy supplied by the battery is 12CV2.ABoth A and R falseBBoth A and R true and R is not correct reason for ACA is true and R is falseDBoth A and R are true and R is correct reason of A.The energy of a charged capacitor is given by the expression (q= charge on the conductor and C= its capacity
Aq22CBq2CC2qCDq2C2
Show that the capacitance of a spherical capacitor is 4πε0b2(b−a) when the outer sphere is charged and the inner earthed.
View SolutionShows these variation of charge q for two capacitors C1 and C2 The two capacitors have the same plate separation. But the plate area of C2 is double than that of C1. Which of the lines in the figure corresponds to C1 and C2 and why?
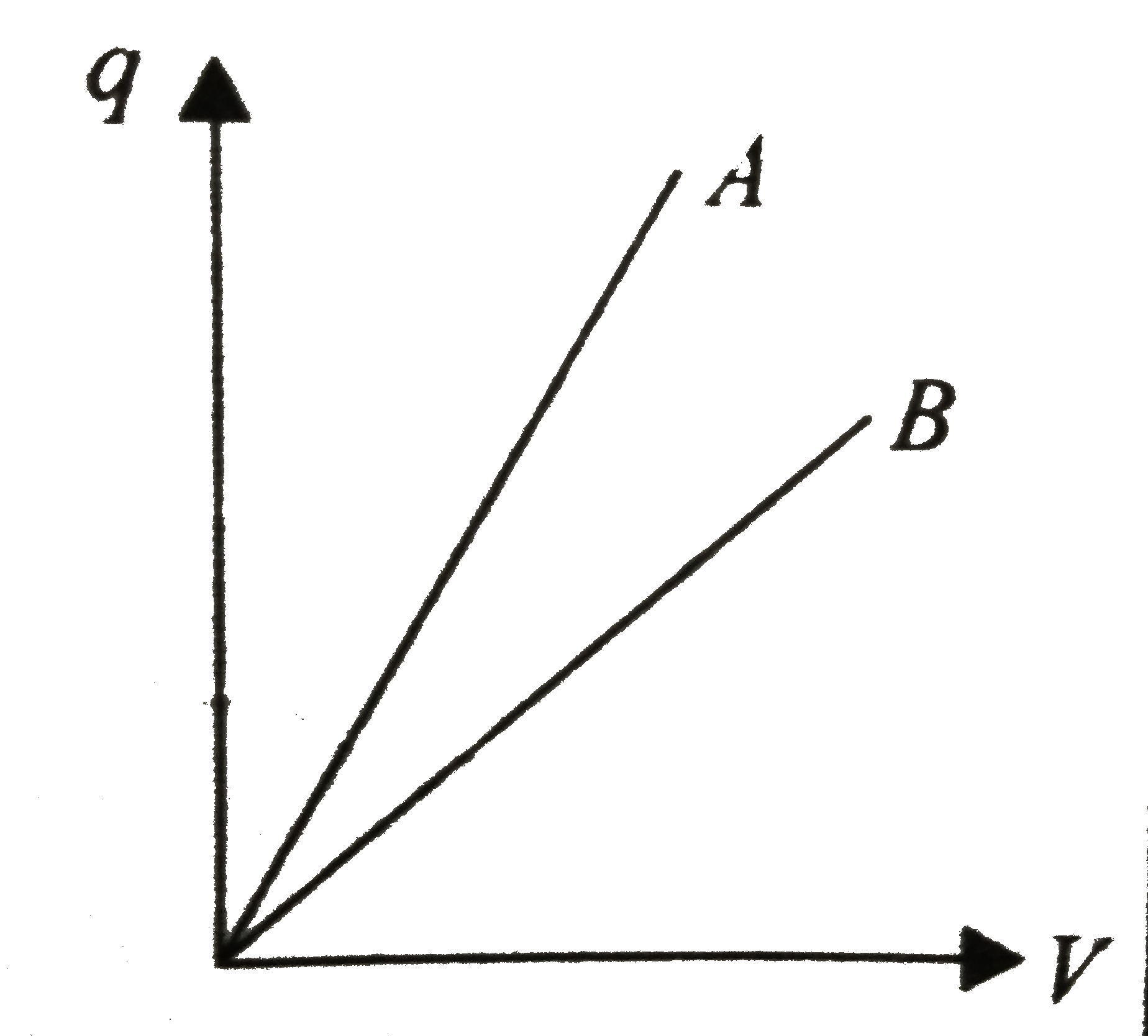 .
.
View SolutionA battery is used to charge a parallel plate combination of two identical capacitors. If the potential difference across the battery is V and the total charge Q flows through the battery during the charging process then 1) The charge on each capacitor is Q/2 and the potential of each capacitor is V/2 2) The charge on each capacitor is Q and the potential of each capacitor is V 3) The charge on each capacitor is Q/2 and the potential of each capacitor is V 4) The charge on each capacitor is Q and the potential of each capacitor is V/2
View SolutionTwo capacitors of equal capacitance (C1=C2) are as shown in the figure. Initially, while the switch is open (as shown) one of the capacitors is uncharged and the other carries charge Q0. The energy stored in the charged capacitor is U0. Sometime after the switch is closed, the capacitors C1andC2 carry charged Q1andQ2 respectively, the energy stored in the capacitors are U1andU2 respectively. Which of the following expression is correct?

View SolutionTwo capacitors of equal capacitance (C1=C2) are shown in the figure. Initially, while the switch S is open, one of the capacitors is uncharged and the other carries charge Q0. The energy stored in the charged capacitor is U0. Sometimes after the switch is colsed, the capacitors C1andC2 carry charges Q1andQ2, respectively, the voltages across the capacitors are V1andV2, and the energies stored in the capacitors are U1andU2. Which of the following statements is INCORRECT ?

View Solution

