Question

State and prove Gauss's law in electrostatics.

Explanation

Gass's theorem : The total normal electric induction (TNEI) over a closed surface is equal to the algebraic sum of the charges, I .e., the net charge, enclosed by the surface.

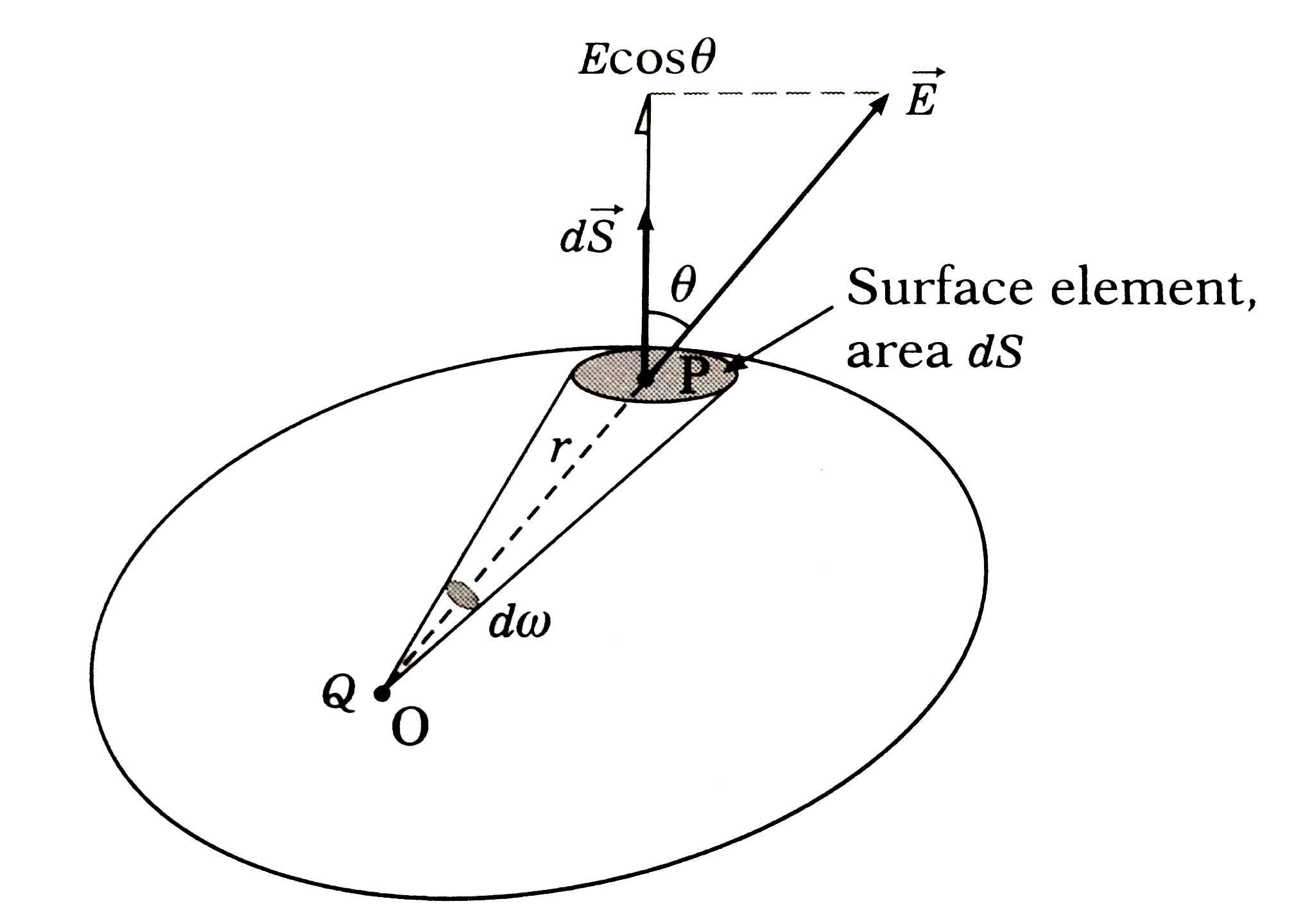
Proof : Consider a closed surface of arbitrary shape surrounding a positive point charge Q, as shown in the figure.
Consider a small element of the surface, of area dS around a point P at a distance r from the point O. The area dS is assumed to be so small that every point on it can be considered to be at the same distance r from O and the electric field over it can be considered to be uniform. The magnitude of the electric field at P is
`E=(Q)/(4pi epsilon r^(2)) " " ` ...(1)
where `epsilon` is the permittivity of the medium surrounding the point charge.
The outward normal `d vec S` drawn to the area element makes an angle `theta` with the electric field. Hence, the total normal electric induction TNEI over area dS
`=epsilon E cos theta dS = epsilon ((Q)/(4pi epsilon r^(2))) cos theta dS =(Q)/(4pi)*(dS cos theta)/(r^(2)) " " `...(2)
`(dS cos theta)/(r^(2))` is the solid angle `d epsilon` subtended by the area dS at O.
`therefore` TNEI over `dS=(Q)/(4pi)d epsilon " " ` ...(3)
` therefore ` TNEI over the closed surface `=oint (theta)/(4pi)d epsilon =(Q)/(4pi)ointd epsilon " " ` ...(4)
A closed surface subtends a solid angle of `4pi` steradians at any point inside it, i.e., `oint d epsilon =4pi` steradians. ` " " ` ...(5)
`therefore` TNEI over the closed surface `=(theta)/(4pi) xx 4pi =Q " " `...(6)
Instead of a single free charge, if there are many free charges, we can write Eq. (6) for each point charge and then sum over all the chares.
`therefore` TNEI over the closed surface `=Sigma Q " " `...(7)
where `Sigma Q` is the algebraic sum of all free charges, i.e., the net charge, enclosed by the surface. This proves Gauss's theorem.