If AD and PS are medians of △ABCand△PQR respectively where △ABC~△PQR, Prove that ABPQ=ADPS.
△ABC is bigger
△PQR is bigger
Both triangles will be equal
cannot be decided
The correct Answer is:A
Step by step video, text & image solution for If AD and PS are medians of triangleABC and trianglePQR respectively where triangleABC ~ trianglePQR, Prove that (AB)/(PQ)=(AD)/(PS). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRIC CONSTRUCTIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - GEOMETRIC CONSTRUCTIONS EXERCISE - Assigment 5.2
4 Videos
- GEOMETRIC CONSTRUCTIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - GEOMETRIC CONSTRUCTIONS EXERCISE - Assigment 5.3
3 Videos
- GEOMETRIC CONSTRUCTIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - GEOMETRIC CONSTRUCTIONS EXERCISE - 5.5 4 marks each
2 Videos
- FINANCIAL PLANNING BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - FINANCIAL PLANNING EXERCISE - ASSIGNEMENT 4.4
4 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - 4 Marks Questions
18 Videos
Similar Questions
Knowledge Check
If △ABC~△PQR and ABPQ=75, then………..
A△ABC is biggerB△PQR is biggerCboth triangles will be equalDcan not be decidedIf G1andG2 are the centroid of △ABCand△PQR respectively, then ¯¯¯¯¯¯AP+¯¯¯¯¯¯BQ+¯¯¯¯¯¯CR=
A¯¯¯¯¯¯¯¯¯G1G2B2¯¯¯¯¯¯¯¯¯G1G2C3¯¯¯¯¯¯¯¯¯G1G2D6¯¯¯¯¯¯¯¯¯G1G2
M and N are the points on sides QR and PQ respectively of a △PQR, right angled at Q. prove that PM2+RN2=PR2+MN2
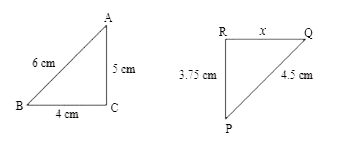
View SolutionIn the given figure, if △ABC~△PQR, find the value of x?
View SolutionIn △ ABC, AD is a median. Prove that AB + AC > 2AD
View SolutionIn figure , if PQ||BCandPR||CD . Prove that ARAD=AQAB .
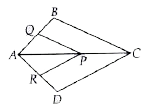
View SolutionIf AD, BE and CF are medians of triangle ABC then prove that median AD divides line segment EF.
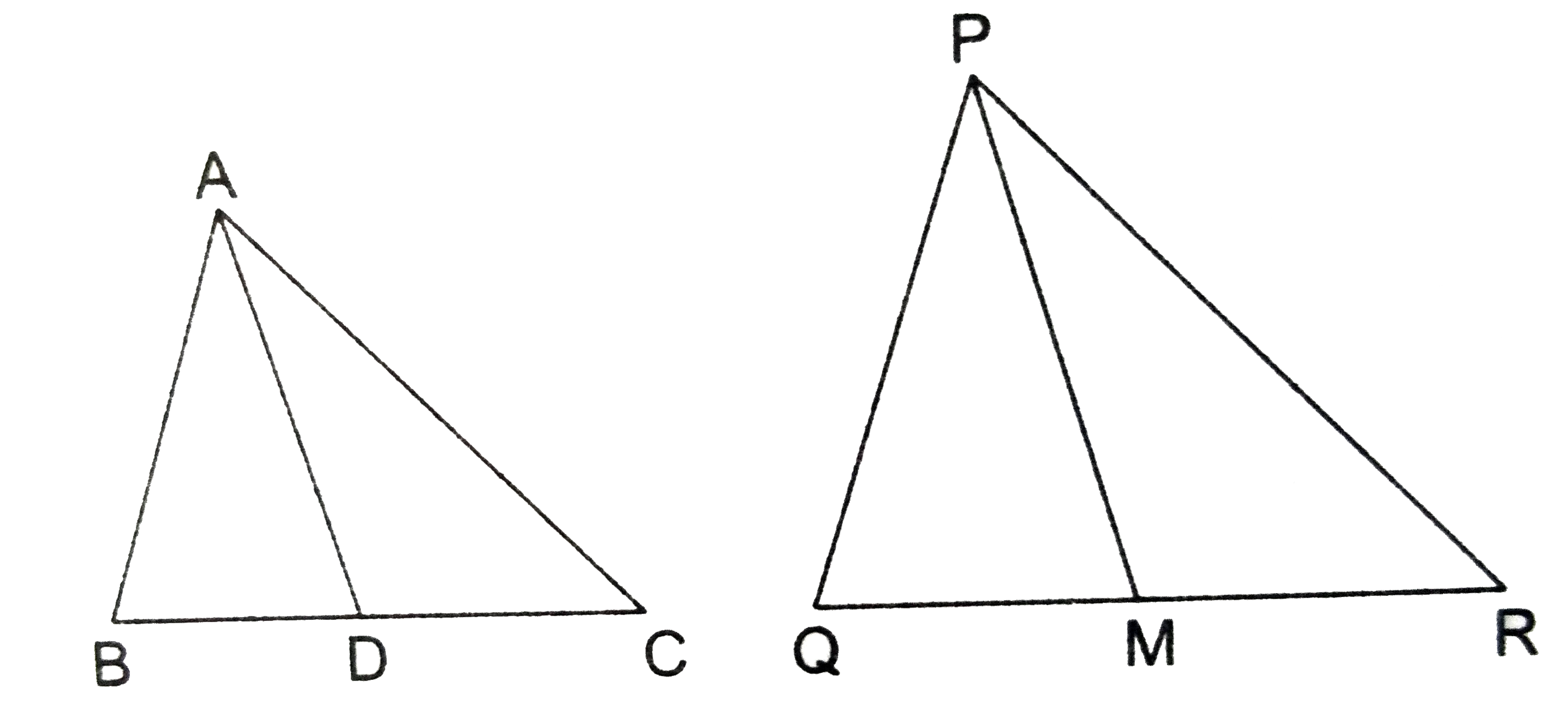
View SolutionSides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Prove that ΔABC~DetlaPQR
View Solution
