An aeroplane at an altitude of 1 km flying horizontally at 800 km/hr passes directly over an observer. Find the rate at which it is approaching the observer when it is 1250 metres away from him.
To solve the problem of finding the rate at which the aeroplane is approaching the observer, we will follow these steps:
Step 1: Understand the given information
- The altitude of the aeroplane (H) = 1 km = 1000 m
- The speed of the aeroplane (dS/dt) = 800 km/hr
- The distance from the observer when we need to find the rate (L) = 1250 m = 1.25 km
Step 2: Set up the relationship using the Pythagorean theorem
In the right triangle formed by the observer, the point directly below the aeroplane, and the aeroplane itself, we have:
- L2=S2+H2
Where:
- L = distance from the observer to the aeroplane
- S = horizontal distance from the observer to the point directly below the aeroplane
- H = altitude of the aeroplane
Step 3: Differentiate the equation
We need to differentiate the equation L2=S2+H2 with respect to time (t):
ddt(L2)=ddt(S2+H2)
Since H is constant, this simplifies to:
2LdLdt=2SdSdt
Dividing both sides by 2 gives:
LdLdt=SdSdt
Step 4: Solve for dLdt
Rearranging the equation gives us:
dLdt=SLdSdt
Step 5: Find the value of S
Using the Pythagorean theorem:
S=√L2−H2
Substituting the known values:
L=1.25 km,H=1 km
S=√(1.25)2−(1)2=√1.5625−1=√0.5625=0.75 km
Step 6: Substitute known values into the equation
Now substitute S, L, and dSdt into the equation:
- S=0.75 km
- L=1.25 km
- dSdt=800 km/hr
dLdt=0.751.25⋅800
Calculating this gives:
dLdt=0.6⋅800=480 km/hr
Final Answer
The rate at which the aeroplane is approaching the observer when it is 1250 meters away is 480 km/hr.
- The altitude of the aeroplane (H) = 1 km = 1000 m
- The speed of the aeroplane (dS/dt) = 800 km/hr
- The distance from the observer when we need to find the rate (L) = 1250 m = 1.25 km
In the right triangle formed by the observer, the point directly below the aeroplane, and the aeroplane itself, we have:
- L2=S2+H2
Where:
- L = distance from the observer to the aeroplane
- S = horizontal distance from the observer to the point directly below the aeroplane
- H = altitude of the aeroplane
We need to differentiate the equation L2=S2+H2 with respect to time (t):
ddt(L2)=ddt(S2+H2)
Since H is constant, this simplifies to:
2LdLdt=2SdSdt
Dividing both sides by 2 gives:
LdLdt=SdSdt
Rearranging the equation gives us:
dLdt=SLdSdt
Using the Pythagorean theorem:
S=√L2−H2
Substituting the known values:
L=1.25 km,H=1 km
S=√(1.25)2−(1)2=√1.5625−1=√0.5625=0.75 km
Now substitute S, L, and dSdt into the equation:
- S=0.75 km
- L=1.25 km
- dSdt=800 km/hr
Calculating this gives:
dLdt=0.6⋅800=480 km/hr
The rate at which the aeroplane is approaching the observer when it is 1250 meters away is 480 km/hr.
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVES BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - APPLICATIONS OF DERIVATIVES EXERCISE - Examples for Practice
61 Videos
- APPLICATIONS OF DERIVATIVES BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - APPLICATIONS OF DERIVATIVES EXERCISE - MULTIPLE CHOICE QUESTIONS
12 Videos
- APPLICATIONS OF DEFINITE INTEGRALS ( AREA ) BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS ( AREA ) EXERCISE - EXAMPLES FOR PRACTICE (3 OR 4 MARKS )
5 Videos
- BINOMIAL DISTRIBUTIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - BINOMIAL DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS
8 Videos
Similar Questions
An aeroplane is flying horizontally at an altitude of 3000 ft directly over an observer. If it is flying with a speed of 300 ft /sec, the rate at which it is moving away from the observer when it is at 5000 ft away from the observer is
View SolutionAn aeroplane is flying horizontally at a height of 23km with a velocity of 15 km/h. Find the rate at which it is receding from a fixed point on the ground which it passed over 2 min ago.
View Solution
Knowledge Check
An aerplane at an altitude of 400 metres, flying horizontally with a speed of 250m/sec, passes directly the observer, it is approaching him at the rate of
A100m/sec.B200m/secC300m/sec.D150m/sec.An aeroplne A is flying horizontally due east at a speed of 400km/hr.Passengers in A, observe another aeroplane B moving perpendicular to direction of motion of A.Aeroplane B is actually moving in a direction 30∘ north of east in the same horizontal plane as shown in the figure.Determine the velocity of B
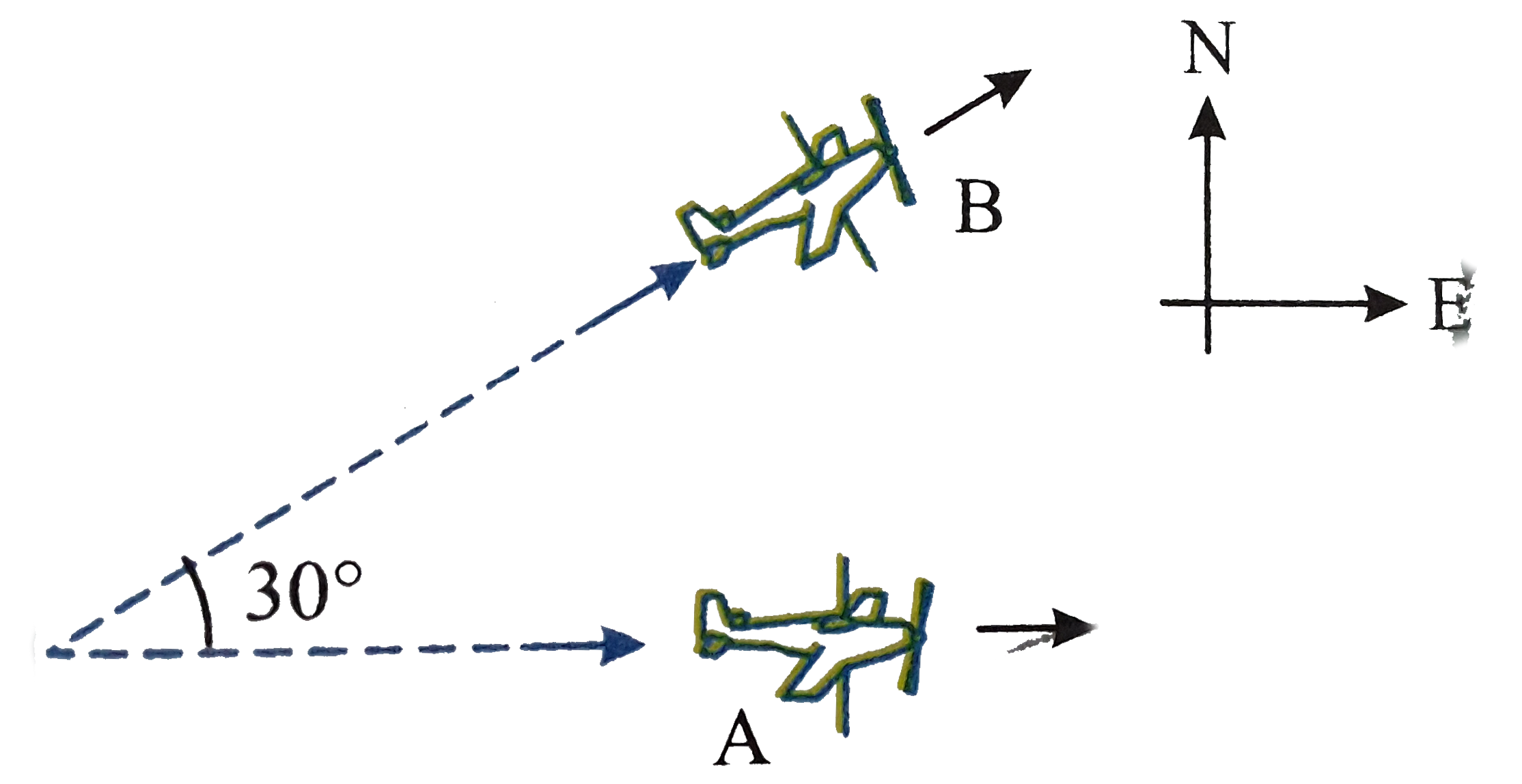 A400√3ˆi+400√3ˆjB400ˆi+400√3ˆjC400ˆi+400ˆjD400√3ˆi+400ˆj
A400√3ˆi+400√3ˆjB400ˆi+400√3ˆjC400ˆi+400ˆjD400√3ˆi+400ˆjAn aeroplane is in a level flight of 144 km/hr at an altitude of 1000 m. How far horizontally from a given target should a bomb be released from it to hit the target ?
A571.43mB671.43mC471.34mD371.34m
A man is walking at the rate of 6.5 km/hr towards the foot of a tower 120m high. At what rate is he approaching the top of the tower when he is 5m away from the tower?
View SolutionA jet plane flies at an altitude of 1 km at a speed twice that of sound. How far away will the plane be from an observer when he first hears it coming?
View SolutionAn aeroplane at an altitude of 1200 metres finds that two ships are sailing towards it in the same direction. The angles of depression of the ships as observed from the aeroplane are 60o and 30o respectively. Find the distance between the two ships.
View SolutionA fightre plane flying horizontally at an altitude oa 1.5km with speed 720h−1 passes directly over head an anticraft gun. At what angle from the vertical should the gun be fired from the shell with muzzle speed 600ms−1 to hit plane. At what minimum altitude showld the pilot fly the plane to avoid being hit ? ( Take g= 10 ms^(-2)).
View SolutionA fighter plane flying horizontally at an altitude of 1.5km with speed of 720kmh9−10 passes directlu overhead an anticraft gun. At what anle fro the gun with muzzle speed 400ms−1 to hit the plane in shortest time ?
View Solution
