The objective function, z=4x1+5x2, subject to 2x1+x2≥7,2x1+3x2≤15,x2≤3,x1,x2≥0 has minimum value at the point
A
On X-axis
B
on Y-axis
C
at the origin
D
on the line parallel to X-axis
Video Solution
Text Solution
The correct Answer is:A
Given objective function is
minimise, z=4x2+5x2
sujbect of constraints, 2x1+x2≥7,
2x1+3x2≤15,
x2≤3
and x1,x2≥0
Table for line 2x1+x2=7 is
x10123x27531
Table for line 2x1+3x2=15
x1036x2531

Now, the value of z at coner points are given below:
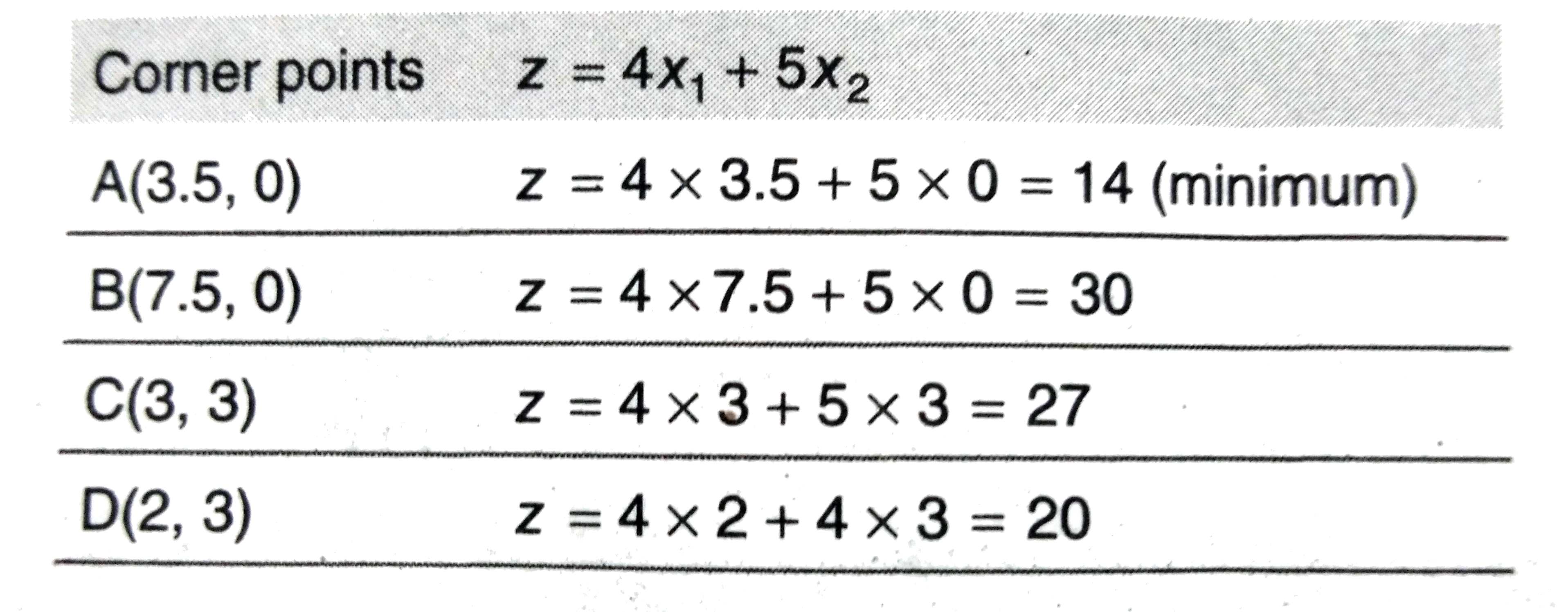
Hence, the minimum value of z is 14 at (3.5,0) i.e., at X-axis.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The objective function Z=4x1+5x2, Subject to 2x1+x2≥7,2x1+3x2≤15,x2≤3,x1,x2≥0 has minimum value at the point
AOn x-axisBOn y-axisCAt the originDOn the line parallel to x-axisThe objective function Z=x1+x2, subject to x1+x2≤10,−2x1+3x2≤15,xx1≤6,x1,x2≥0 has maximum value ________ of the feasible region .
AAt only one pointBAt only one pointsCAt every point of the segment joining two pointsDAt every points of the line joining two pointsThe LPP problem Max z=x1+x2 such that −2x1+x2≤1,x1≤2,x1+x2≤3andx1,x2≥0 has
AOne solutionBThree solutionsCInfinite number of solutionsDNo solution
Maximize z=x1+3x2
Subject to
3x1+6x2≤8
5x1+2x2≤10
and x1,x2≥0
View SolutionMinimize z=−x1+2x2
Subject to
−x1+3x2≤10
x1+x2≤6
x1−x2≤2
and x1,x2≥0
View SolutionFor the LPP Min z=x1+x2 such that inequalities
5x1+10x2≥0,x1+x2≤1,x2≤4 and x−1,x2≥0
View SolutionFor L.P.P. maximize z=4x1+2X2 subject to 3x1+2x2≥9,x1−x2≤3,x1≥0,x2≥0 has ……
View SolutionThe minimum value of z=2x1+3x2 subjected to the constraints 2x1+7x2≥22,x1+x2≥6,5x1+x2≥10 and x1,x2≥0, is
View Solution
