The minimum value of subjected to the constraints and , is
14
20
10
16
The correct Answer is:A
Given,
the shaded region is the required region.
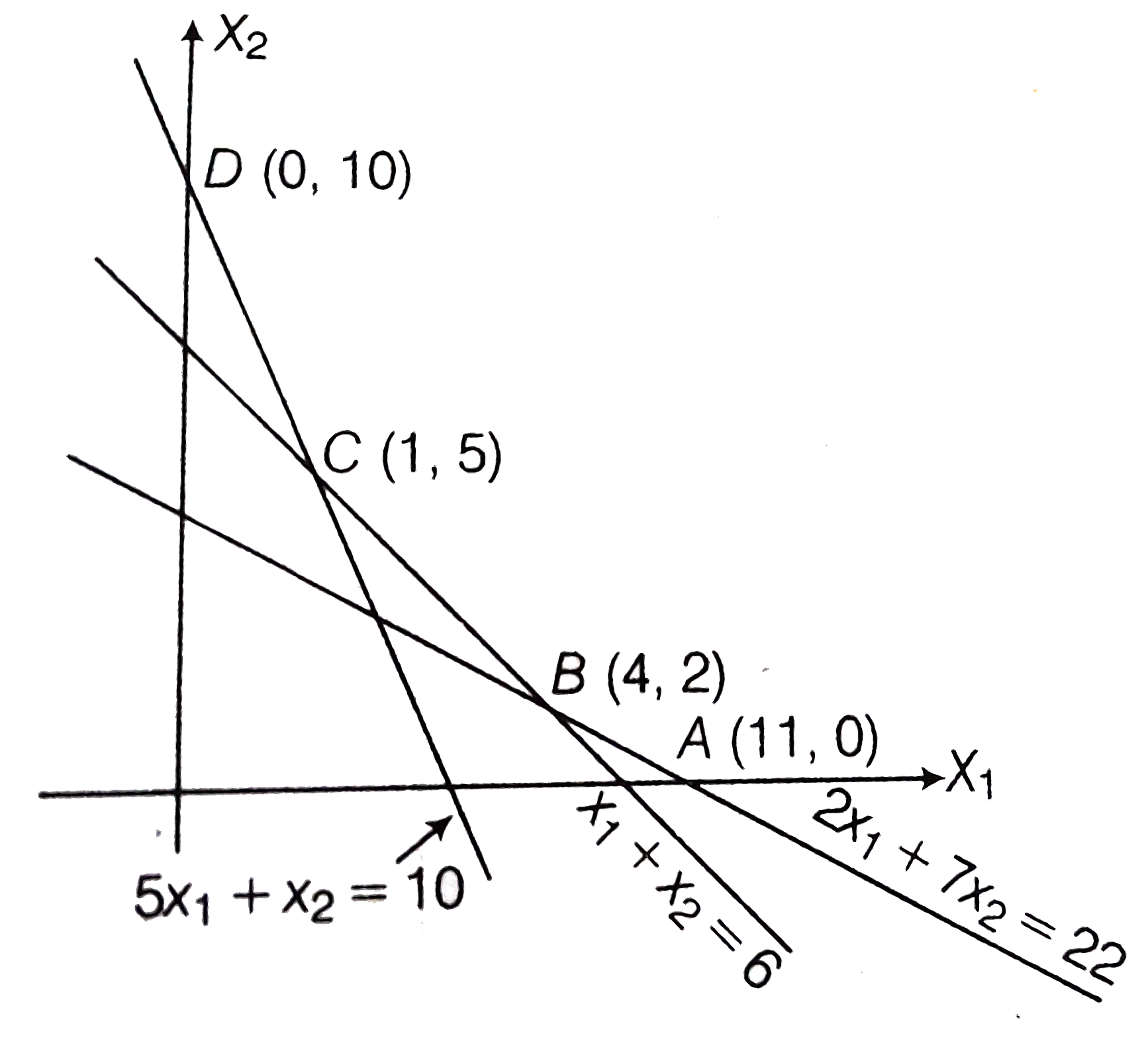
Now,
.
Minimum value of z is 14.
Related Playlists
Similar Questions
The minimum value of Z=2x1+3x2, subject to the constraints 2x1+7x2≥22,x1+x2≥6,5x1+x2≥10 and x1,x2≥0, is
View SolutionThe minimum vlaue Z=2x1+3x2 subject to the conditions 2x1+7x2≥22,x1+x2≥6,5x1+x2≥10 and x1,x2≥0 is
View SolutionMinimize z=−x1+2x2
Subject to
−x1+3x2≤10
x1+x2≤6
x1−x2≤2
and x1,x2≥0View SolutionFor the LPP Min z=x1+x2 such that inequalities
5x1+10x2≥0,x1+x2≤1,x2≤4 and x−1,x2≥0View SolutionFind maximum value of z=2x+3y subject to the constraints x+y≤4,x≥0,y≥0 .
View SolutionBy graphical method, the solutions of linear programming problem maximise Z=3x1+5x2 subject to constraints 3x1+2x2≤18,x1≤4,x2≤6x1≥0,x2≥0 are
View SolutionThe maximum value of z = 4x +2y subject to the constraints 2x+3y≤18,x+y≥10,x,y≥0 is
View SolutionThe linear programming problem : Maximize z=z=x1+x2 subject to constraints x1+2x2≤2000,x1+x2≤1500,x2≤600,x1≥0 has
View SolutionMaximize z=x1+3x2
Subject to
3x1+6x2≤8
5x1+2x2≤10
and x1,x2≥0View SolutionThe minimum value of Z=4x+5y subjected to the constraints x+y≥6,5x+y≥10,x≥0,y≥0 is
View Solution


