The curve xy = 1 is symmetrical
A
about x-axis
B
about y-axis
C
about both the axis
D
about origin
Video Solution
Text Solution
The correct Answer is:D
Given, xy = 1
Putting -x for x and -y for y in the given equation the curve remains same. Thus, the curve is symmetric about origin.
|
Topper's Solved these Questions
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - Exercise 2
34 Videos
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner
6 Videos
- APPLICATIONS OF DERIVATIVESBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MHT CET CORNER
21 Videos
Similar Questions
Knowledge Check
If f(x) is an even function, then the curve y=f(x) is symmetric about
Ax-axisBy-axisCboth the axesDnone of theseIf f(x) is an odd function, then the curve y=f(x) is symmetric
Aabout x-axisBabout y-axisCabout both the axesDin opposite quadrantsWhich of the following curve is symmetrical about origins ?
A B
B C
C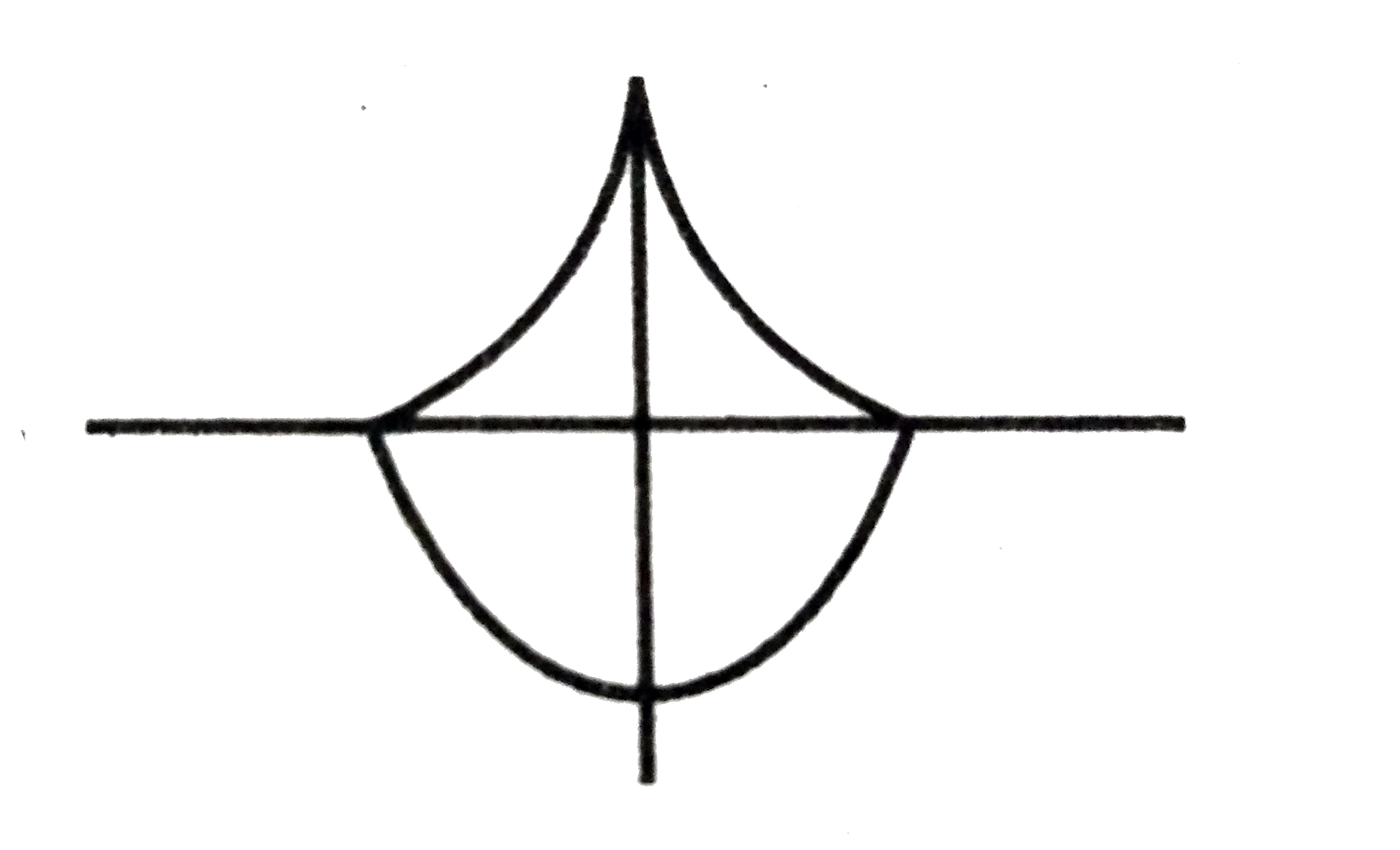 D
D
STATEMENT-1: The curve y=−x22+x+1 is symmetric with respect to the line x =1. because
STATEMENT-2 : A parabola is symmetric about its axis.
View Solution8x2+11xy+bt2 is a symmetric expression, then b = ______
View SolutionFind the derivative of y(x)=x3/(x+1)2 with respect to x .
View SolutionThe value of n for which the length of the subnormal of the curve xyn=an+1 is constant
View SolutionThe normal at anypoint P (ct,c/t) on the curve xy = c2 meets the curve at Q(ct1,c/t1), then t1=
View Solution