Which of the following is a linear objective ? A) z=ax+by B)z≤ax+by C) z>ax+by D)z≠ax+by
Z= ax + by
Z≤ax+by
Z>ax+by
Z≠ax+by
The correct Answer is:A
Linea function Z=ax + by where , a and b are constants which has to be maximised or minimised, is called a linear objetive function.
Topper's Solved these Questions
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 1 (TOPICAL PROBLEMS )(Solution of LPP Graphical Method )
15 Videos
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 2 (MISCELLANEOUS PROBLEMS )
30 Videos
- LINEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - LINEEXERCISE - MHT CET Corner
3 Videos
- MATHEMATICAL LOGIC BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER
22 Videos
Similar Questions
The feasible region of a system of linear inequalities is shown shaded in the following graph . If the objective function is Z = ax + by where a,b are constants and the maximum of Z occurs at points A and D then :
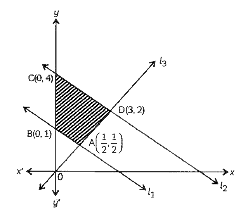
View SolutionEvaluate each of the following algebraic expressions for x=2, y=−3, z=−2, a=2, b=3: (i) ax+by+z
View Solution
Knowledge Check
The equation of the plane through the line of intersection of planes:
ax + by + cz + d = 0, ax + b'y + c z + d' = 0 and parallel to the line y = 0, z = 0 is:A(ab'−a'b)x+(bc'−b'c)y+(ad'−a'd)=0B(ab'−a'b)x+(bc'−b'c)y+(ad'−a'd)z=0C(ab'−a'b)y+(bc'−b'c)z+(ad'−a'd)=0Dnone of theseConsider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?AI and IVBII and IIICI and IIIDII and IVLet the feasible region of the linear programming problem with the objective function Z = ax + by is unbounded and let M and m be the maximum and minimum value of Z, respectively. Now, consider the following statements
I. M is the maximum value of Z, if the open half plane determined by ax + by gt M has no point in common with the feasible region. Otherwise, Z has no maximum value.
II. mis the minimum value of Z, if the open half plane determined by ax + by lt m has no point in common with the feasible region. Otherwise, Z has no minimum value. Choose the correct option.AOnly I is true .BOnly II is trueCBoth I and II are trueDNeither I nor II is true
In a LPP, the maximum value of the objective function Z = ax +by is always finite.
View SolutionThe equation of the plane through the line of intersection of the planes ax+by+cz+d=0 and a'x+b'y+c'z+d'=0 parallel to the line y=0 and z=0 is
View SolutionThe solutions of the equations, where a+b+c≠0
(b+c)(y+z)−ax=b−c
(c+a)(z+x)−by=c−a
(a+b)(x+y)−cz=a−b are ….
View SolutionIf a:b:c=(y−z):(z−x):(x−y) then the value of ax + by + cz is
View SolutionIf we represent the linear equations x + y - z = 3, 2x + 3y + z = 10 and 3x - y - 7z = 1 in matrix form as AX = B, then AT is:
View Solution
