The direction rations of the diagonals of a cube which joins the origin to the opposite corner are (when the three concurrent edges of the cube are coordinate axes)
(2√2,2√3,2√3)
(1,1,1)
(2,-2,1)
(1,2,3)
The correct Answer is:B
Let the length of side of cube be a
Then, coordinates of conner P opposite to origin are (a,a,a)
∴ Direction ratios of diagonal OP are a -0, a-0, a-0 i..e.,a,a,i.,1,1.
Topper's Solved these Questions
- THREE DIMENSIONAL GEOMETRYBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - MHT CET Corner
3 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - MHT CET Corner
3 Videos
- STRAIGHT LINE BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STRAIGHT LINE EXERCISE - EXERCISE 2(MISCELLANEOUS PROBLEMS)
30 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - EXERCISE 2 (MISCELLANEOUS PROBLEMS)
26 Videos
Similar Questions
Find the angle between the diagonals of a cube with edges of length "a".
View SolutionA cube is placed so that one corner is at the origin and three edges are along the x-,y-, and ,z-axes of a coordinate system (figure).Use vector to compute
a.The angle between the edge along the z-axis (line ab) and the diagonal from the origin to the opposite corner (line ad).
b. The angle between line ac (the diagonal of a face ) and line ad.
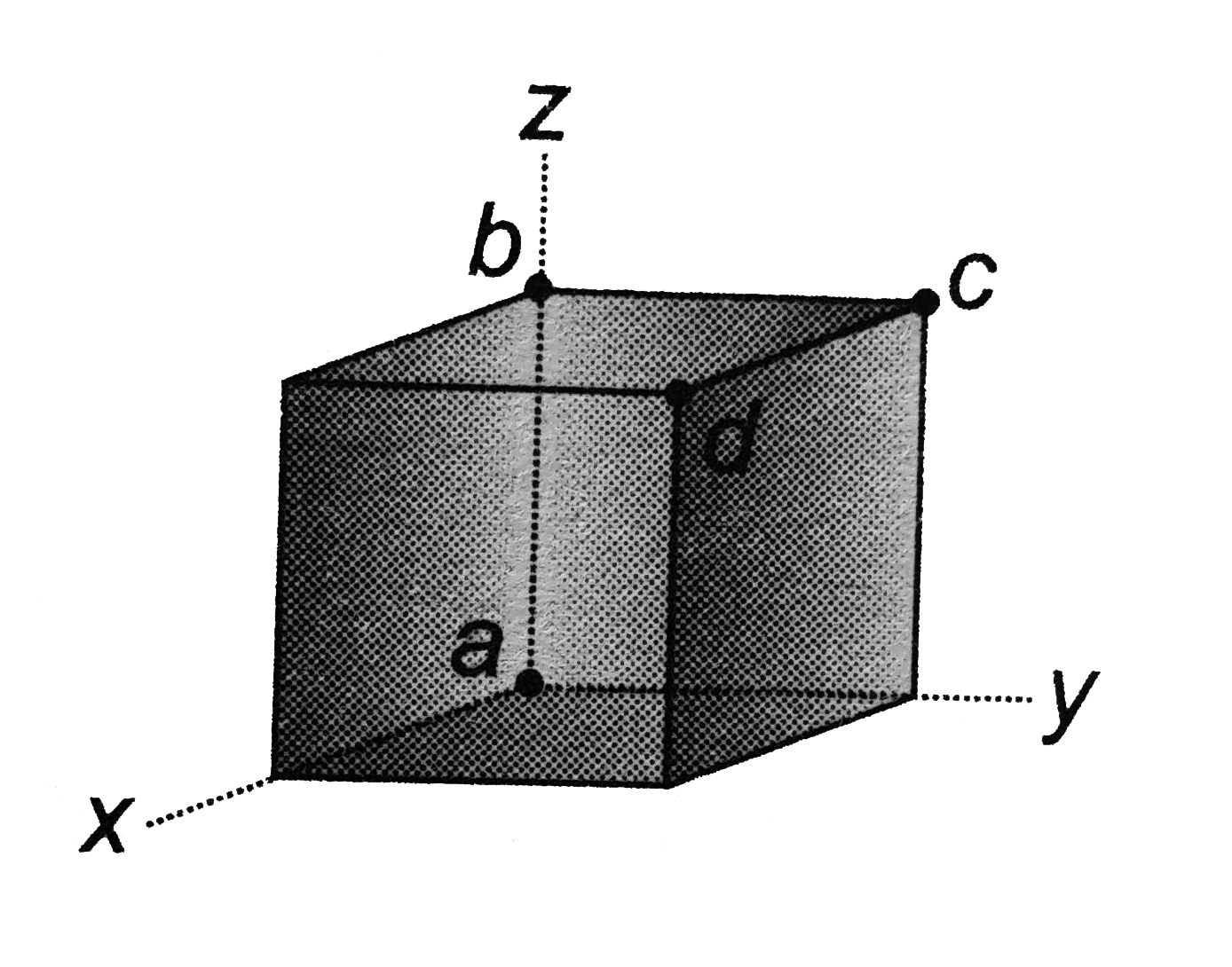
View Solution
Knowledge Check
The direction rations of the diagonals of a cube which joins the origin to the opposite corner are (when the three concurrent edges of the cube are coordinate axes)
A2√3,2√3,2√3B1,1,1C2,-2,1D1,2,3If the length of the diagonal of a cube is 6√3 cm , then length of the edge of the cube is 3 cm .
A2 cmB3 cmC6 cmD36√3 cmIf each edge of a cube is 6 cm, then find the diagonal of cube.
A6√2cmB6√3cmC36√2cmD36√3cm
If the length of the diagonal of a cube is 6√3 cm , then length of the edge of the cube is
View SolutionThe shortest distance between a diagonal of a unit cube and the edge skew to it, is
View SolutionThe angle between a diagonal of a cube and one of its edges is
View SolutionWhich of these is the length of the longest diagonal of a cube of edge a.
View SolutionIf three concurrent edges of a parallelopiped of volume V represent vectors →a,→b,→c then the volume of the parallelopiped whose three concurrent edges are the three concurrent diagonals of the three faces of the given parallelopiped is
View Solution
