Find the angle between the diagonals of a cube with edges of length "a".

Video Solution

Text Solution

Verified by Experts

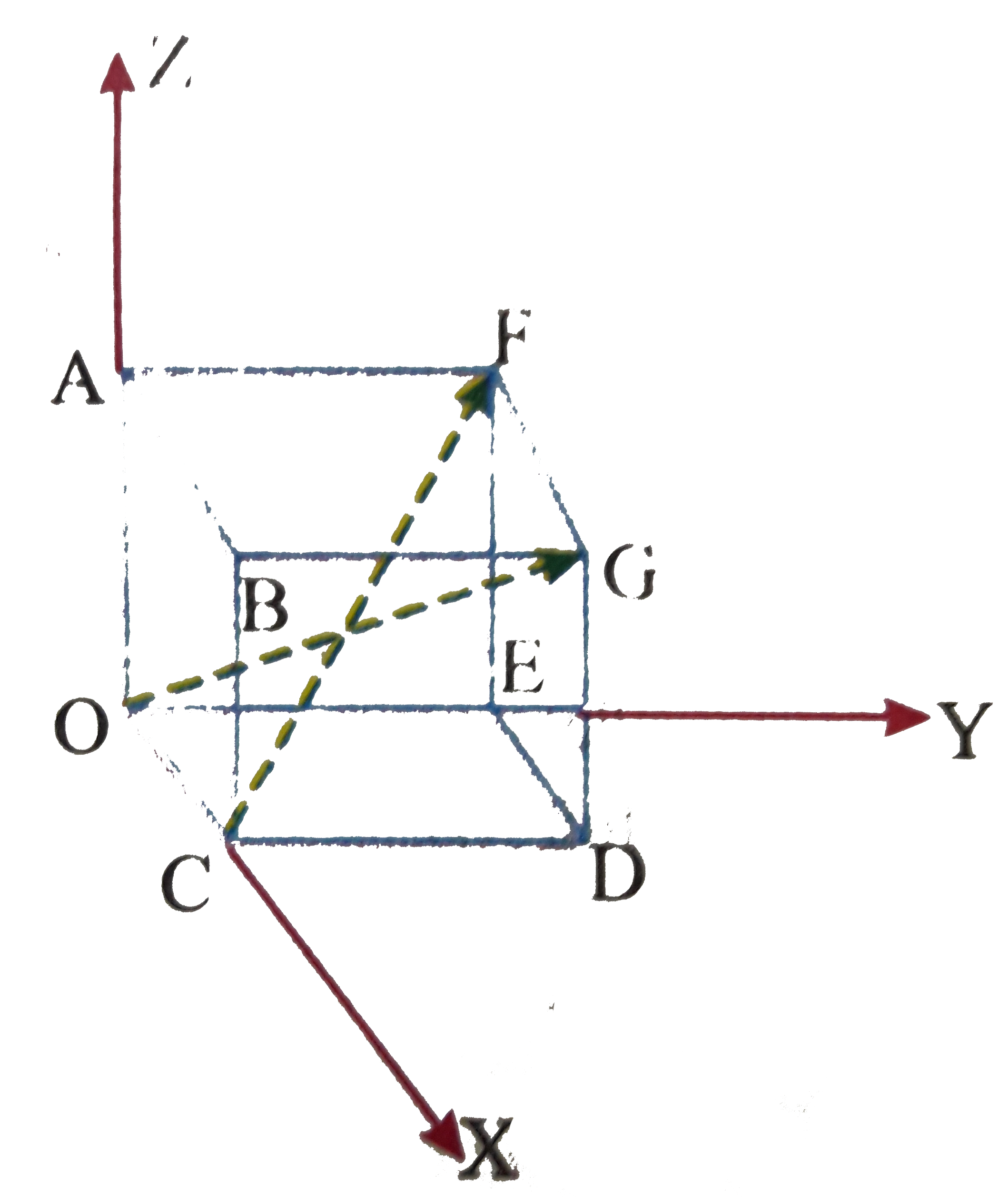
From the diagram
$¯ ¯¯¯¯ ¯ O G = ¯ ¯¯ ¯ d_{1} = α ˆ i + α ˆ j + α ˆ k, ¯ ¯¯¯¯ ¯ C F = ¯ ¯¯ ¯ d_{2} = - α ˆ i + α ˆ j + α ˆ k$
$∴$ The angle angle between the diagonals is
$cos θ = \frac{{\to d}_{1} . {\to d}_{2}}{∣ ∣ {\to d}_{1} ∣ ∣ . ∣ ∣ {\to d}_{2} ∣ ∣} = \frac{1}{3} \Rightarrow θ = {cos}^{- 1} (\frac{1}{3})$

|

Updated on:21/07/2023

Class 11 PHYSICS VECTOR

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The angle between two diagonals of a cube İs
A ${cos}^{- 1} (\frac{1}{3})$
B $30^{\circ}$
C ${cos}^{- 1} (\frac{1}{\sqrt{3}})$
D $45^{\circ}$
Question 2 - Select One
The angle between two diagonals of a cube will be
A ${sin}^{- 1} (\frac{1}{3})$
B ${cos}^{- 1} (\frac{1}{3})$
Cvariable
Dnone of these
Question 3 - Select One
The angle between two diagonals of a cube will be
A ${sin}^{- 1} (\frac{1}{3})$
B ${cos}^{- 1} (\frac{1}{3})$
Cvariable
Dnone of these

NARAYNA-VECTORS-LEVEL-II (H.W)

Home
Ask Doubt
Profile