The perpendicular bisector of the line segment joining P (1, 4) and Q (k, 3) has yintercept −4 . Then a possible value of k is (1) 1 (2) 2 (3) −2 (4) −4

A

−4

B

1

C

2

D

−2

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

Since slope of PQ = 4−31−k=11−k
slope of AM = (k-1)
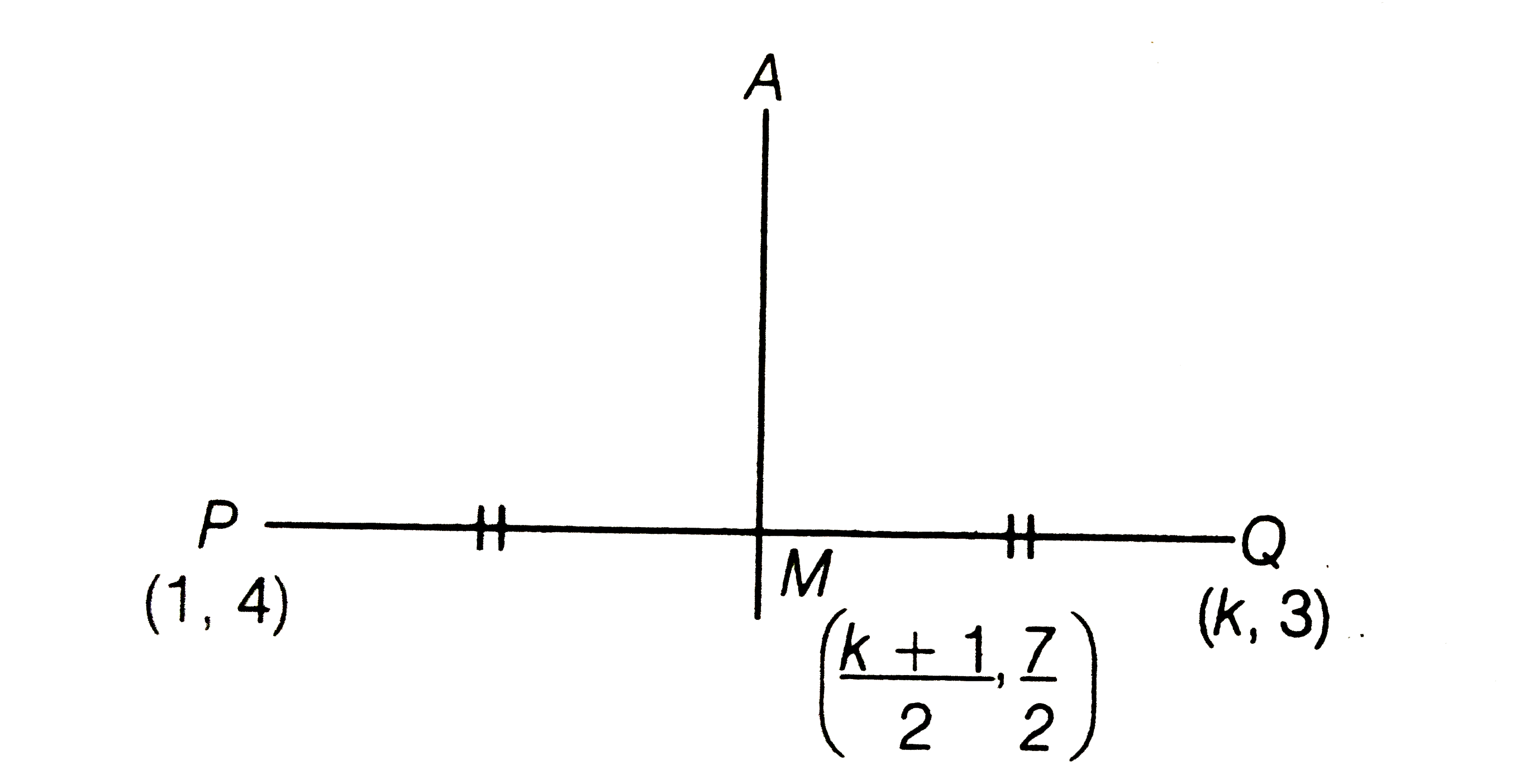
ocr_image
Equation of AM is
y−72=(k−1)[x−(k+12)]
For y-intercept , when x=0 m y=-4 then
−4−72=−(k−1)(k+12)
⇒152=k2−12⇒k2−1=15
k=−+4

Updated on:21/07/2023
|
Class 12MATHSSTRAIGHT LINE

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The perpendicular bisector of the line segment joining the points A(1,5) and B(4,6) cuts the Y-axis at

    A(0,13)
    B(0,-13)
    C(0,12)
    D(13,0)

  • The perpendicular bisector of the line segment joining A(1, 4) and B(t, 3) has y - intercept equal to −4. Then, the product of all possible values of t is equal to

    A1
    B2
    C−16
    D−4

  • The equation of the perpendicular bisector of line segment joining points A (4,5) and B (−2,3) is :

    A2x−y+7=0
    B3x+2y−7=0
    C3x−y−7=0
    D3x+y−7=0