If a cone of maximum volume is inscribed in a given sphere, then the ratio of the height of the cone to the diameter of the sphere is $3 / 4$ (b) $1 / 3$ (c) $1 / 4$ (d) $2 / 3$

A

$\frac{2}{3}$

B

$\frac{3}{4}$

C

$\frac{1}{3}$

D

$\frac{1}{4}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Let, the diameter of the sphere be AE = 2r
Let the radius of cone is x and height is y.

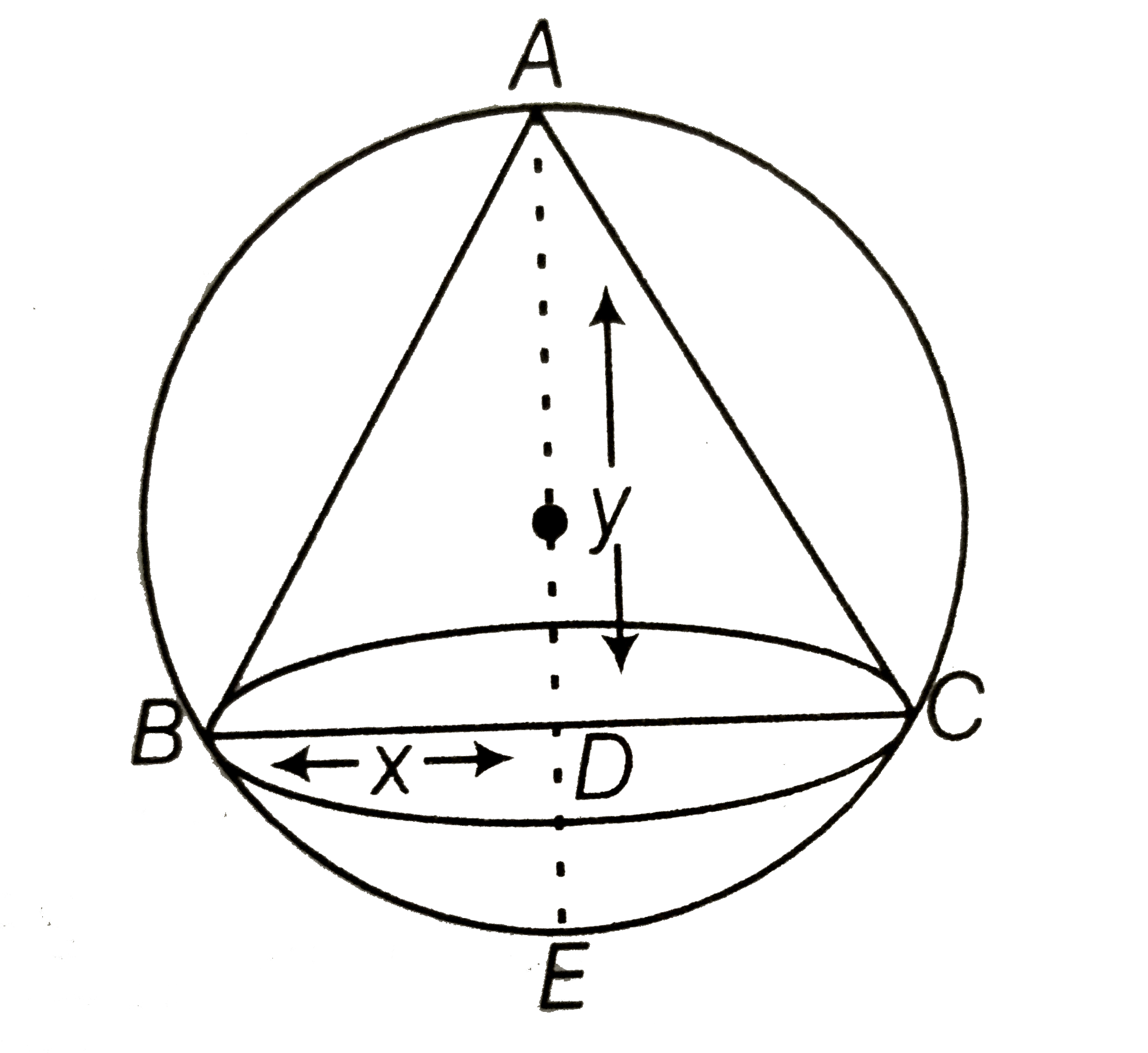
$∴ A D = y$
since, $B D^{2} = A D \cdot D E$
$\Rightarrow x^{2} = y (2 r - y)$ …(i)
volume of cone,
$V = \frac{1}{3} π x^{2} y = \frac{1}{3} π y (2 r - y) y$
$= \frac{1}{3} π (2 r y^{2} - y^{3})$
On differentiating w.r.t y, we get
$\frac{d V}{d y} = \frac{1}{3} π (4 r y - 3 y^{2})$
For maxima and minima , put $\frac{d V}{d y} = 0$
$\Rightarrow \frac{1}{3} π (4 r y - 3 y^{2}) = 0$
$\Rightarrow y (4 r - 3 y) = 0$
$\Rightarrow y (4 r - 3 y) = 0$
$\Rightarrow y = \frac{4}{3} r, 0$
Again differentiating, we get
$\frac{d^{2} V}{{d y}^{2}} = \frac{1}{3} π (4 r - 6 y)$
At $y = \frac{4}{3} r, \frac{d^{2} V}{{d y}^{2}} = \frac{1}{3} π (4 r - 8 r) = - v e$
$∴$ Volume of cone is maximum at $y = \frac{4}{3} r$
Now, ratio = $\frac{Height of cone}{Diameter of sphere}$
$= \frac{y}{2 r} = \frac{4 r / 3}{2 r} = \frac{2}{3}$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Show that the cone of the greatest volume which can be inscribed in a given sphere has an altitude equal to 2/3 of the diameter of the sphere.
A $2 / 3$
B $3 / 4$
C $1 / 3$
D $1 / 4$
Show that the cone of the greatest volume which can be inscribed in a given sphere has an altitude equal to 2/3 of the diameter of the sphere.
A $2 / 3$
B $3 / 4$
C $1 / 3$
D $1 / 4$
If a right circular cone, having maximum volume is inscribed in a sphere of radius 3cm, then the curved surface area (in $c m^{2}$ ) of this cone is
A $6 \sqrt{3 π}$
B $6 \sqrt{2} π$
C $8 \sqrt{2} π$
D $8 \sqrt{3} π$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-PRACTICE SET 15-PAPER 2 (MATHEMATICS)

Home
Ask Doubt
Profile