Show that the cone of greatest volume which can be inscribed in a given sphere is such that three times its altitude is twice the diameter of the sphere. Find the volume of the largest come inscribed ina sphere of radius R.
Video Solution
Text Solution
Let R be the radius of the given sphere with centre O, and let V be the volume of the inscribed cone, h be its height and r be the radius of the base.
In the given figure, we have OD=AD−AO=(h−R)
∴R2=(h−R)2+r2orr2=h(2R−h)
Now, V=13πr2h=13πh2(2R−h) [using (i)]
∴dVdh=13πh(4R−3h),andd2Vdh2=(43πR−2πh)
For a maxima or minima, we have dVdh=0
Now, dVdh=0⇒13πh(4R−3h)0
⇒h=0or(4R−3h)=0⇒h=43R [∵h≠0]
And, [d2Vdh2]h=(4/3)R=−4πR3<0
So, V is maximum when h=43R, i.e., when 3h=2(2R)
i.e., 3 times the height = 2 times the diameter
Volume of the largest cone =13π×16R29×(2R−4R3)=32πR381
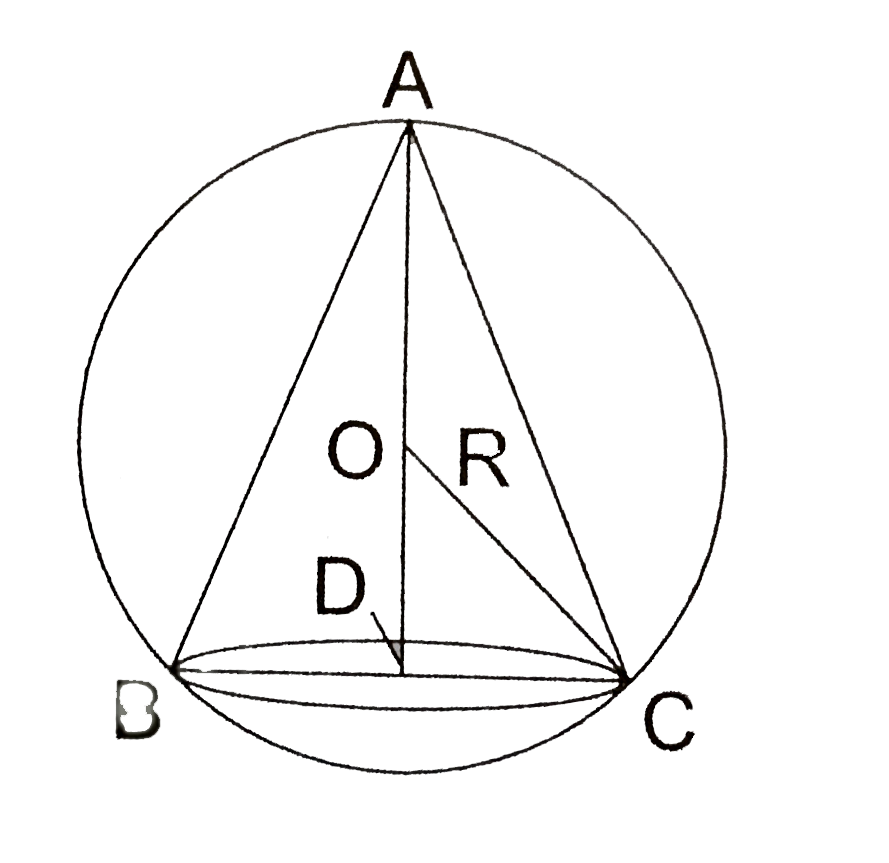
|
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 11A
21 Videos
- APPLICATIONS OF DERIVATIVESBOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 11B
17 Videos
- ADJOINT AND INVERSE OF A MATRIXBOOK - RS AGGARWALCHAPTER - ADJOINT AND INVERSE OF A MATRIXEXERCISE - Exercise 7
37 Videos
- AREA OF BOUNDED REGIONS BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 17
39 Videos
Similar Questions
Knowledge Check
Height of greatest cone inscribed in a sphere of radius r is
A2r3Br3C3r2D4r3Show that the cone of the greatest volume which can be inscribed in a given sphere has an altitude equal to 2/3 of the diameter of the sphere.
A2/3B3/4C1/3D1/4Show that the cone of the greatest volume which can be inscribed in a given sphere has an altitude equal to 2/3 of the diameter of the sphere.
A2/3B3/4C1/3D1/4
Find the volume of the larges cylinder that can be inscribed in a sphere of radius rcm.
View SolutionThe diameter of a sphere is 1 cm. Find its volume.
View SolutionFind the volume of a sphere of radis r.
View SolutionThe height of the cone of maximum volume inscribed in a sphere of radius R is
View SolutionThe diameter of a sphere is 14 cm. Its volume is
View Solution
