A random variable X can attain only the value 1,2,3,4,5 with respective probabilities k,2k,3k,2k,k. if m is the mean of the probability distribution, then (k,m) is equal to
A
(3,19)
B
(19,3)
C
(18,4)
D
(1,3)
Video Solution
Text Solution
The correct Answer is:B
We know sum of probability distribution is 1.
∴x+2k+3k+2k+k=1⇒k=19
∴Mean, m=5∑i=1pixi
=k(1)+2k(2)+3k(3)+2k(4)+k(5)
=k(1+4+9+8+5)=19×27=3
∴(k,m)=(19,3)
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
A number k is selected from the set {1, 2, 3, 4, ……10}. If k2−4k+3<0 then the probability is
A15B25C310D110Let X be a random variable which takes values k with the probability kp. where k = 1, 2, 3, 4 and p ∈(0,1) . Then the standard deviation of X is :
A√7B√10C3D1If the three points (k,2k ) (2k,3k) (3,1 ) are collinear, then k is equal to
A−2B1C12D−12
If a random variable "X" takes values (−1)k2kk,k=1,2,3,... with probabilities P(X=k)=12k, then E(X)
View SolutionA discrete random variable X has the probability distribution as given below
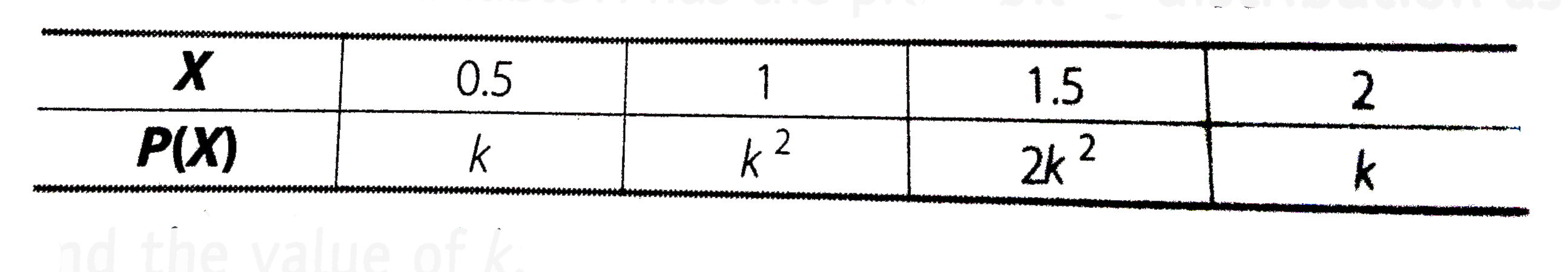
(i) Find the value of k.
(ii) Determine the mean of the distribution.
View SolutionA discrete random variable X can take all possible integer values from 1 to K each with a probability 1K Its variance is
View SolutionHCF of k, 2k, 3k, 4k, and 5k is
View SolutionThe following is the probability distribution of a random vaiable X.
The value of k is
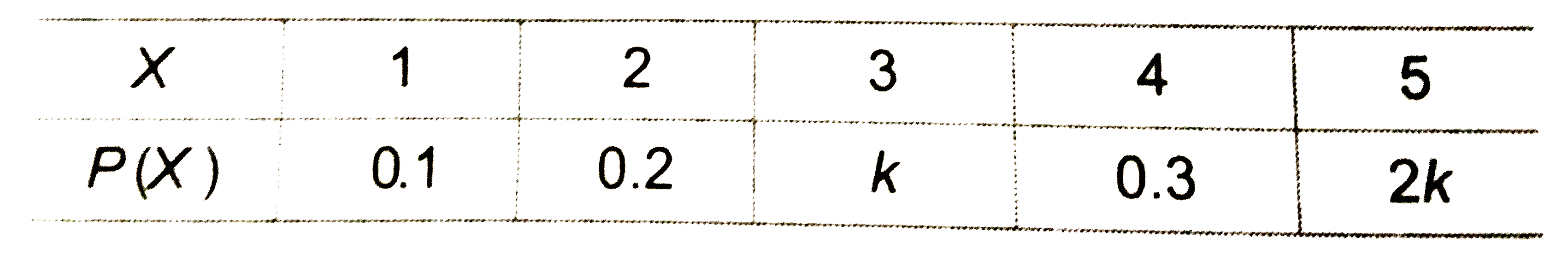
View Solution

