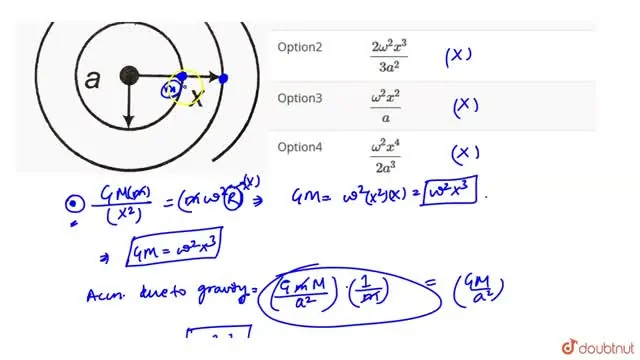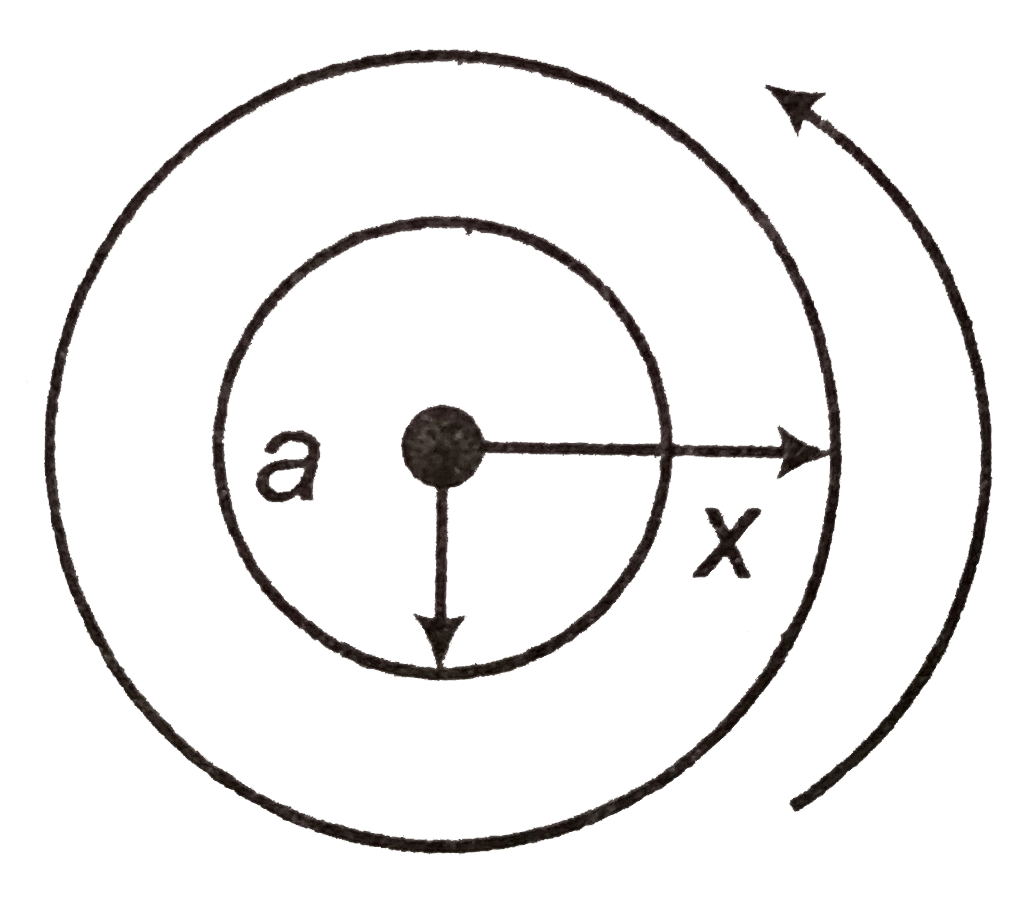
The radius of a planet is a. satelite revolves around it in a circle of radius x with angular velocity $ω$ . The acceleration due to the gravity on planet's surface is

A

$\frac{ω^{2} x^{3}}{a^{2}}$

B

$\frac{2 ω^{2} x^{3}}{3 a^{2}}$

C

$\frac{ω^{2} x^{2}}{a}$

D

$\frac{ω^{2} x^{4}}{2 a^{3}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

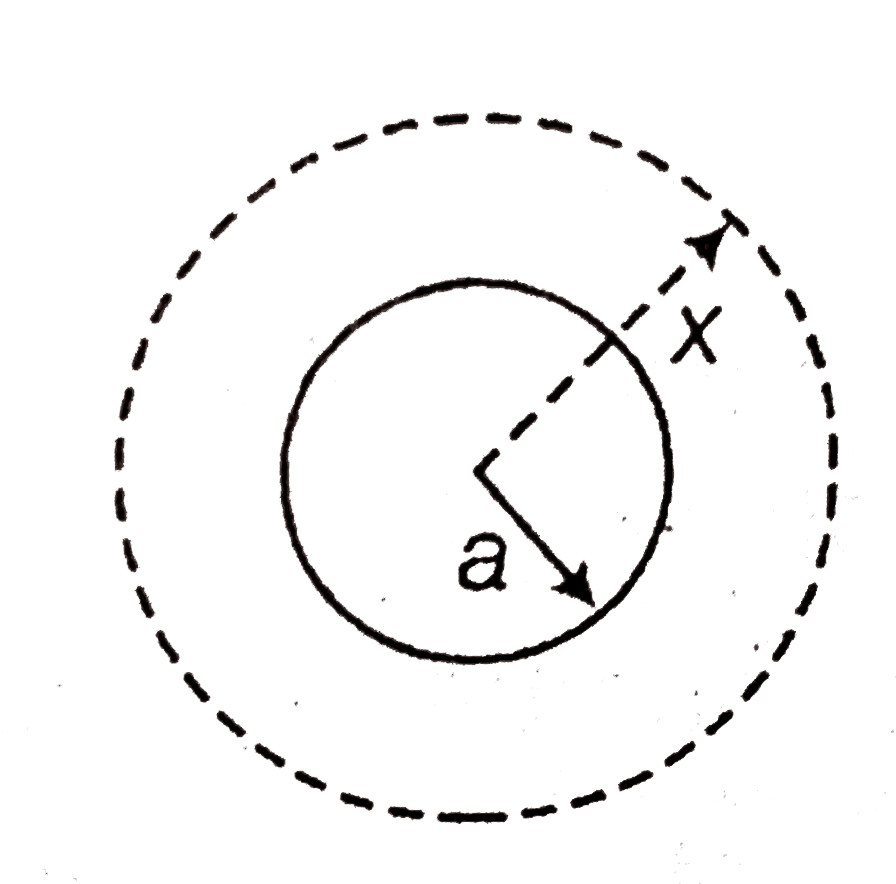
$\frac{G M m}{x^{2}} = m ω^{2} ξ m p l i e s G M = ω^{2} x^{3}$
$g a^{2} = ω^{2} x^{3} [∵ \frac{G m^{2}}{a^{2}} = g]$
$\Rightarrow g = \frac{ω^{2} x^{3}}{a^{2}}$

|

Updated on:21/07/2023

Class 12 PHYSICS PRACTICE SET 06

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The radius of a planet is $R$ . A satellite revolves around it in a circle of radius $r$ with angular velocity $ω_{0}$ . The acceleration due to the gravity on planet's surface is
A $\frac{r^{3} ω_{0}}{R}$
B $\frac{r^{3} ω_{0}^{2}}{R^{2}}$
C $\frac{r^{3} ω_{0}^{2}}{R}$
D $\frac{r^{3} ω_{0}^{2}}{R^{2}}$
Question 2 - Select One
The radius of a planet is n times the radius of earth (R). A satellite revolves around it in a circle of radius 4nR with angular velocity $ω$ . The acceleration due to gravity on planet's surface is
A $R ω^{2}$
B16 $R ω^{2}$
C $32 n R ω^{2}$
D $64 n R ω^{2}$
Question 3 - Select One
The mass of a planet is twice the mass of earth and diameter of the planet is thrie the diameter of the earth, then the acceleration due to gravity on the planet's surface is
A $g / 2$
B $2 g$
C $2 g / 9$
D $3 g / \sqrt{2}$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-PRACTICE SET 06-PAPER 1 (PHYSICS & CHEMISTRY)

Home
Ask Doubt
Profile