The headlights of a truck are 1.22 m apart and light of wavelength 5000 Å is used for the headlights. The pupil of the eye of the obeserver has a diameter of 1 mm. what should be the maximum distance of the truck from observer, so that the headlights are just separated for him?
2 km
1.5 km
3 km
3.5 km
The correct Answer is:A
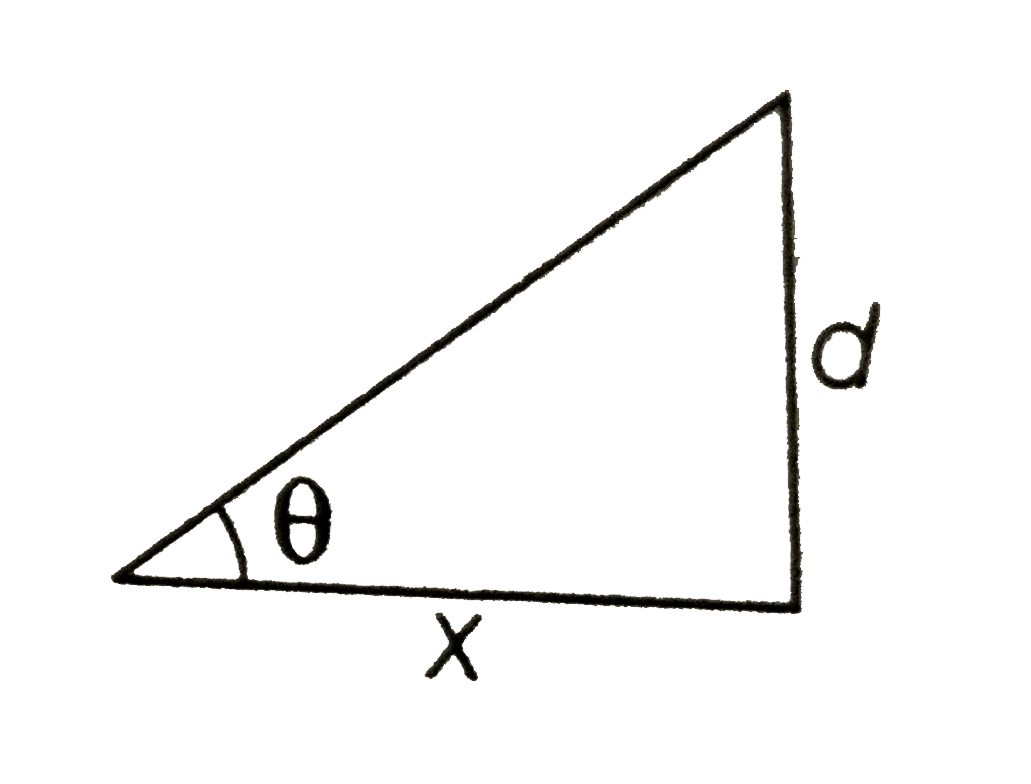
Let D=diameter of the eye lens, d=distance between the two sources and distance of the truck=x
R.P. of the eye, 1θ=D1.22λ
but tanθ=θ=dx∴1θ=xd
∴xd=D1.22λ∴x=Dd1.22λ
∴x=(1×10−3×1.22λ)
∴x=1×10−3×1.221.22×5000×10−10
=10−3×1075<br>=2x10^(3)m=2km
Topper's Solved these Questions
Similar Questions
In YDSE, light of wavelength 5000Å is used. The third bright band on the screen is formed at a distance of 1cm from the central bright band. If the screen is at a distance of 1.5m from the centre of narrow slits, calculate the separation between the slits.
View SolutionLight of wavelength 5000 Å is incident on a slit of width 0.1 mm. Find out the width of the central bright line on a screen distance 2m from the slit?
View Solution
Knowledge Check
The head lights of a jeep are 1.2 m apart. If the pupil of the eye of an observer has a diameter of 2 mm and light of wavelength 5896Å, is used, what should be the maximum distance of the jeep from the observer if the two head lights are just separated ?
A33.4 kmB33.4 mC3.34 kmD3.34 mLight d of wavelength 5000Å is incident normally on a slite. The first minimum of the distance of 5 mm from the central maximum on a screen placed at a distance of 2 m from the slit. The width of slit is
A0.1mmB0.2mmC0.3mmD0.4mmThe resolving power of a telescope whose lens has a diameter of 1.22 m for a wavelength of 5000Å is
A2×105B2×106C2×102D2×104
In Young's experiment , the distance of the screen from the two slits is 1.0 m . When a light of wavelength 6000 Å is allowed to fall on the slits , the width of the fringes obtained on the screen is 2.0 mm . Determine (a) the distance between the two slits and (b) the width of fringe if the wavelength of the incident light is 4800 Å.
View SolutionLight of wavelength 5000Å is incident normally on a slit. The first minimumof the diffraction pattern is formed at adistance of 5 mm from centra maximum. The screen is situated at a distance of 2 m from the slit. The slit width is
View SolutionWhat is the resolving power of a telescope whose objective lens has a diameter 1.22 m from a wavelength 4000 Å?
View SolutionLight of wavelength 5000×10−10m is incident normally pattern is observed to lie at distance of 5 mm from the central maximum on screen place at a distance of 3 from the slit. Then the width of the slits is
View SolutionFor the situation of the previous question, find the maximum distance at which the eye would be able to resolve the two headlights of a car which are at a distance of 1.5m.
View Solution

