For the situation of the previous question, find the maximum distance at which the eye would be able to resolve the two headlights of a car which are at a distance of .
(a)
(b)
(c)
(d)
The correct Answer is:B
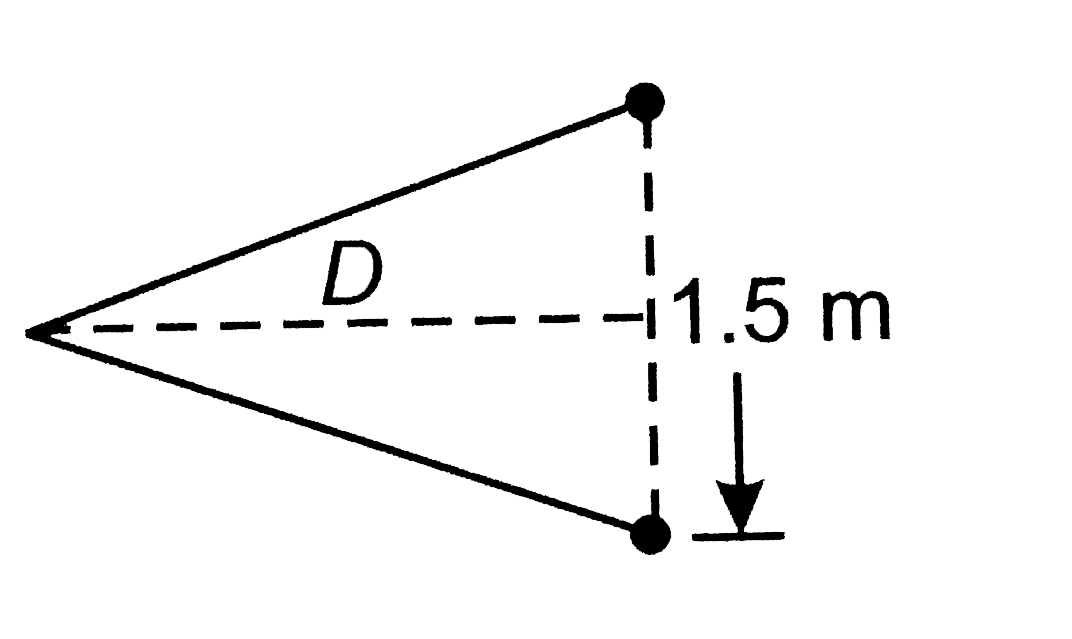
.
Topper's Solved these Questions
- WAVE OPTICSBook:A2ZChapter:WAVE OPTICSExercise:Section B - Assertion Reasoning
Explore 23 Videos
- WAVE OPTICSBook:A2ZChapter:WAVE OPTICSExercise:AIPMT/NEET Questions
Explore 22 Videos
- WAVE OPTICSBook:A2ZChapter:WAVE OPTICSExercise:Polarisation Of Light
Explore 37 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBook:A2ZChapter:SOURCE AND EFFECT OF MAGNETIC FIELDExercise:Section D - Chapter End Test
Explore 30 Videos
Similar Questions
Knowledge Check
A person's salary has increased from rs. 14400 to rs. 16200. What is the percentage increase in his salary?
Aa. 25%Bb. 12.5%Cc. 20%Dd. 35%In the previous question ( number 19). Find the probability that none of the two will be able to solve the problem.
A1315B415C215D2330In previous question, if the total distance covered by the car is s, the maximum speed attained by it will be :
A(2s.a1a2a1+a2)12B(2s.a1a2a1−a2)12C(s2.a1a2a1+a2)12D(s2.a1a2a1−a2)12
Assuming that a car whose CG is at a height b from the rear wheel and at a distance c from the front wheel and at a height h above the pavement, has sufficient power and there is sufficient friction, find the maximum acceleration that it would be able to develop without tipping over backward.
View SolutionThe ciliary muscles can change the focal length of the eye lens. Find the ratio of focal lengths of the eye lens when it is focused on two different objects, one at a distanace of 2 m and the other at a distanc of 1 m. The diameter of normal eye is 2.5 cm.
View Solution
Consider the situation shown in figure. Find distance of image of P from eye E.
View SolutionIn the previous question, if the pitch of the helical path is equal to the maximum distance of the particle from the x-axis
View SolutionTwo point white dots are 1mm apart on a black paper. They are viewed by eye of pupil diameter 3mm. Approximately, what is the maximum distance at which these dits can be resolved by the eye? [Take wavelelngth of light =500nm]
View Solution

