Two electromagnetic waves are moving in free space whose electric field vectors are given by →E1=→E0ˆjcos(kx−ωt) & →E2=→E0ˆkcos(ky−ωt). A charge q is moving with velocity →v=0.8cˆj. Find the net Lorentz force on this charge at t=0 and when it is at origin
qE0(0.4ˆi+0.2ˆj+0.2ˆk)
qE0(0.8ˆi+ˆj+0.2ˆk)
qE0(0.6ˆi+ˆj+0.2ˆk)
qE0(0.8ˆi+ˆj+ˆk)
The correct Answer is:B
NA
Topper's Solved these Questions
Similar Questions
In an electromagnetic wave the electric field vector and magnetic field vector are given as →E=E0ˆi and →B=B0ˆk respectively. The direction of propagation of electromagnetic wave is along:
View SolutionThe electric field of a plane electromagnetic wave is given by
→E=E0(ˆx+ˆy)sin(kz−ωt)
Its magnetic field will be given by :
View Solution
Knowledge Check
Electric field strength →E=E0ˆi and →B=B0ˆi exists in a region. A charge is projected with a velocity →v=v0ˆj origin, then
AIt moves along helix with constant pitchBIt moves along circular path in Y Z planeCIt moves along helix with increasing pitchDIt moves along helix with decreasing pitchElectric field in space is given by −−→E(t)=E0i+j√2cos(ωt+Kz). A positively charged particle at (0,0,πK) is given velocity v0ˆk at t = 0. Direction of force acting on particle is
Af = 0Bantiparallel to ˆi+ˆj√2Cparallel to ˆi+ˆj√2DˆkThe electric field component of a monochromatic radiation is given by
→E=2E0ˆicoskzcosωt
Its magnetic field →B is then given by :A2EocˆjsinkzcosωtB−2EocˆjsinkzsinωtC2EocˆjsinkzsinωtD2Eocˆjcoskzcosωt
The electric field of a plane electromagnetic wave propagating along the x direction in vacuum is →E=E0ˆjcos(ωt−kx) . The magnetic field →B, at the moment t=0 is :
View SolutionIn a certain region, uniform electric field E=−E0ˆk and magnetic field B=B0ˆk are present. At time t=0, a particle of mass in and charge q is given a velocity v=v−0ˆj+v−0ˆk. Find the minimum speed of the particle and the time when it happens so.
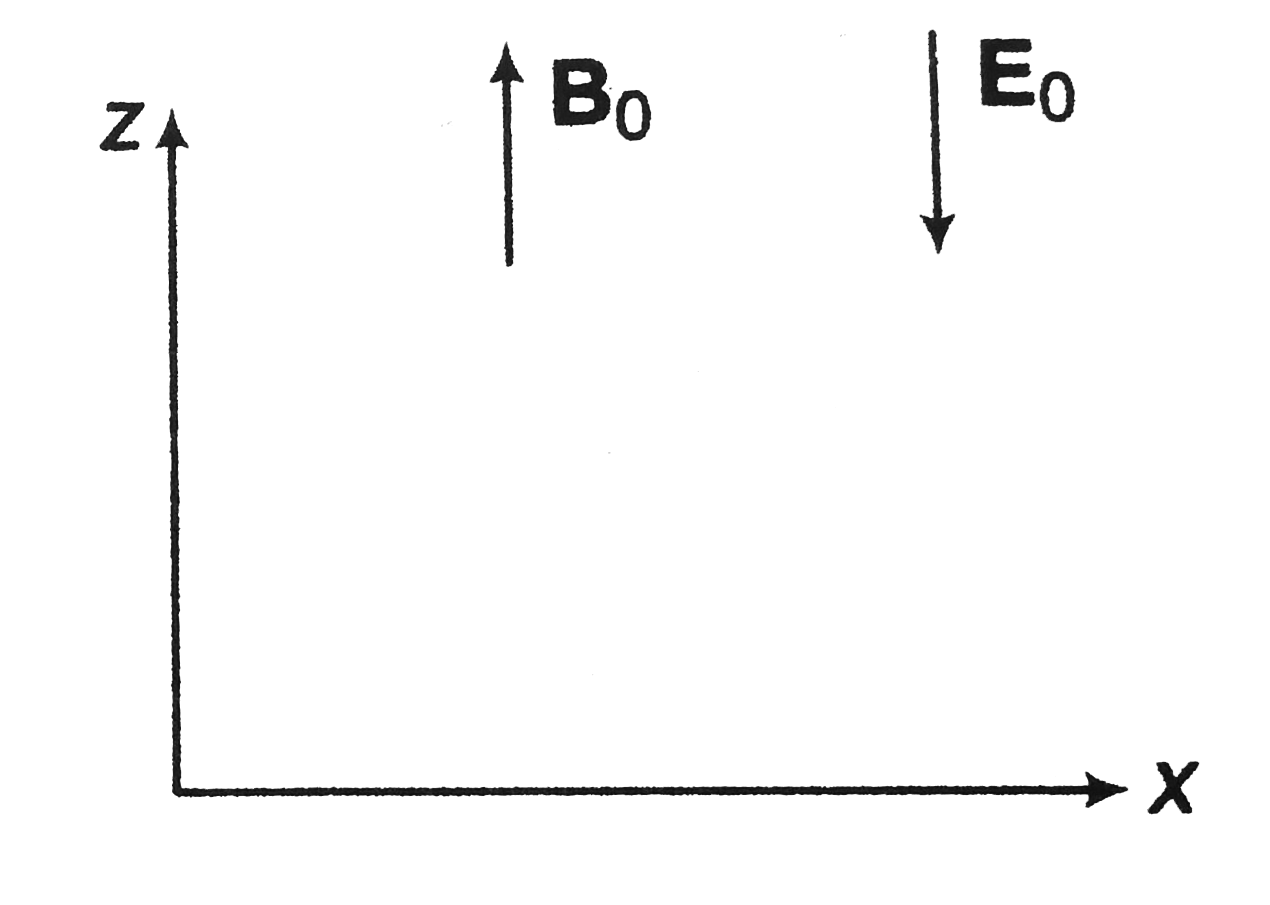
View SolutionThe space has electromagnetic field which is given as →B=−B0ˆk and →E=E0ˆk. A charged particle having mass m and positive charge q is given velocity v0ˆi at origin at t=0sec. The z coordinate of the particle when it passes through the z−axis is (neglect gravity through motion)
View SolutionConsider an object of mass m moving in free space with velocity given by →v=v0cosωtˆi+v0sinωtˆj . .Herev_(0) and omega are constants and t represents time. calculate force acting on object and angle between force and momentum.
View SolutionElectric field of an electromagnetic wave →E=E0cos(ωt−kx)ˆj . The equation of corresponding magnetic field at t=0 should be
View Solution

