Question

Prove using vectors: Medians of a triangle are
concurrent.

Explanation

Let ABC be a triagle and let D,E,F be the mid points of its sides BC, CA and AB respectively. Let `veca,vecb,vec c` be the position vector of A,B and C AB respectively. Then, the position vector of D,E and F are `(vecb+vecc)/(2),(vec c+veca)/(2)` and `(veca+vecb)/(2)` respectively.

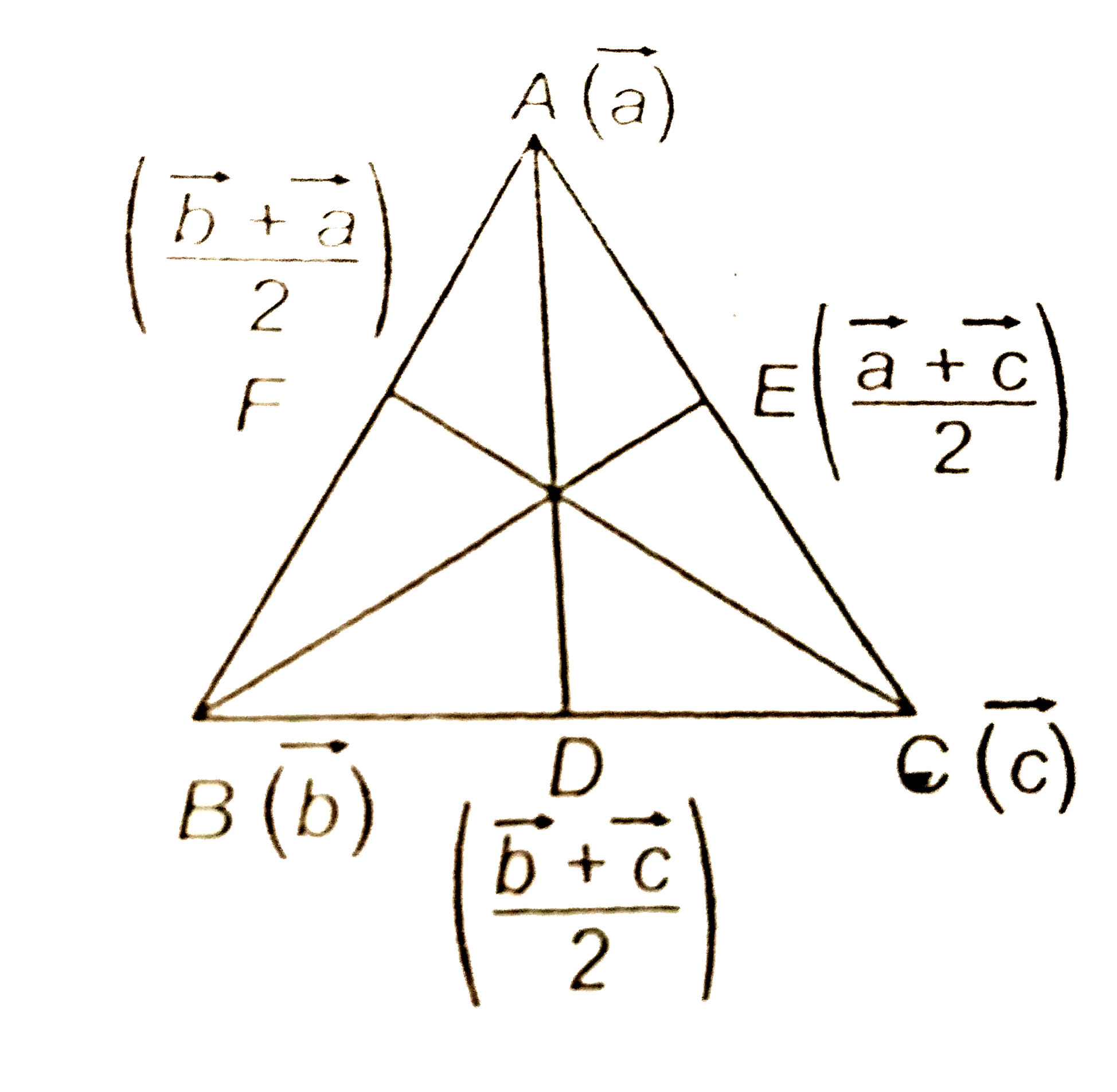
The position vector of a point dividing AD in the ratio `2:1` is
`(1.veca+((vecb+c)/(2)))/(1+2)=(veca+vecb+vecc)/(3)`
Similarly, position vectors of points dividing BE and CF in the ratio `2:1` are each equal to `(veca+vecb+vecc)/(3)`.Thus, the point dividing AD is the ratio `2:1` also divides BE and CF in the same ratio.Hence, the medians of a triangle are concurrent and position vector of centroid is `(veca+vecb+vecc)/(3)`