In Class XI of a certain school, there are 30 students in a Mathematics class and 20 students in Biolog class. Find the number of students which are in Mathematics class or in Biology class in the following cases:
(i) Two classes are conducted at the same time.
(ii) Two classes are condcuted at different time and 5 students study both the subject
Let M be the set of students in Mathematics class.
Let B be the set of students in Biology class
(i) n(M)=30, n(B)=20
Both classes conducted at same time, no student an attend both classes).
Topper's Solved these Questions
- SETS BOOK - AAKASH INSTITUTECHAPTER - SETS EXERCISE - Try yourself
50 Videos
- SETS BOOK - AAKASH INSTITUTECHAPTER - SETS EXERCISE - SECTION-A(Objective Type Questions (One option is correct))
41 Videos
- SETS BOOK - AAKASH INSTITUTECHAPTER - SETS EXERCISE - SECTION-I(Aakash Challengers Questions)
5 Videos
- SEQUENCES AND SERIES BOOK - AAKASH INSTITUTECHAPTER - SEQUENCES AND SERIES EXERCISE - Assignment (SECTION - J) Aakash Challengers
12 Videos
- STATISTICSBOOK - AAKASH INSTITUTECHAPTER - STATISTICSEXERCISE - Section-C Assertion-Reason
15 Videos
Similar Questions
There are 20 students in a Chemistry class and 30 students in a Physics class . Find the number of students which are either in Physics class or Chemistry class in the following cases :
(i) the classes meet at the same hour
(ii) the two classes meet at rolled in both the subjects.
View SolutionThe given bar graph, shows the number of students in different classes.
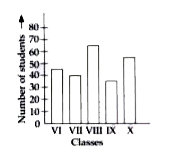
Find the total number of students in the classes VIII to X.
View Solution
Knowledge Check
In a class of 60 students, 30 students like Mathematics, 25 like Science and 15 like both. Then, the number of students who like either Mathematics or Science is
A30B40C45D50A concept learnt by a student in mathematics class is used by her in Geography class. This is an example of
Apositive transferBnegative transferCzero transferDNone of the aboveThere are 20 students in a chemistry class and 30 students in a physics class. If ten students are to be enrolled in both the courses, then the number of students which are either in physics class or chemistry class is
A50, if two classes meet at the same hourB40, if two classes meet at different hoursCboth (a) and (b) correctD(a) correct but (b) incorrect
In a class of 60 students, 30 passed in Physics and 24 passed in Biology. Find the maximum number of students who could have failed in both the subjects
View SolutionIn a class of a certain school, 50 stduents offered mathematics , 42 offered biology and 24 offered both the subjets. Find the number of students offfereing.
(i) mathematics only,
(ii) biology only,
(iii) any of the two subjects.
View SolutionIn a class of 50 students 32 likes Mathematics , 24 like Science and 12 like both . Find the number of students who like neither of the two subjects.
View SolutionThere are 40% girls in a class of 50 students. Find the number of boys in the class
View Solution800 chocolates were distributed among the students of a class. East student got twice as many chocolates as the number of students in the class. The number of students in the class was:
View Solution
