Question

Find area bounded by curves $y=\sqrt{2-x^2}$ and y = |x|.

Explanation

`A_(1) : y = sqrt((2-x^(2))` represents semi-circle
`A_(2) : y = |x|`
Now curve is

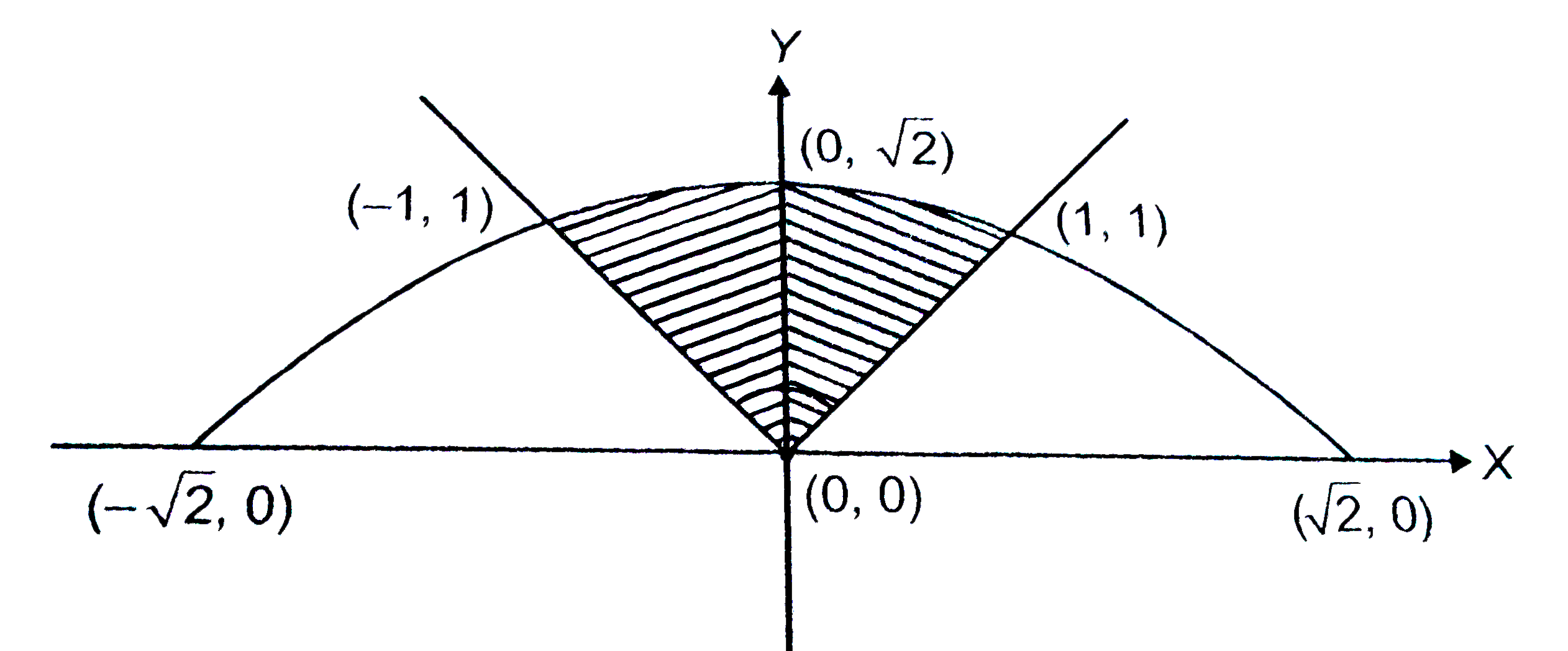
Clearly both curve are symmetrical about Y-axis
Cut point of y = |x| and y = `sqrt(2- x^(2))` is (1,1) and (-1,1)
= `2 underset(0)overset(1)(sqrt(2-x^(2)) - x ) dx`
= `2 [(x)/(2) sqrt(2-x^(2)) + (2)/(2) sin^(-1)"" (x)/(sqrt2) - (x^(2))/(2)]_(0)^(1)`
`= 2 [(1)/(2) + (pi)/(4) - (1)/(2)]`
`= (pi)/(2)` sq. unit
Case II :
If two curve y = f(x) and g(x) and the lines x = a and x = b enclose the area along with the x-axis shown in the figure

Then the required area = `underset(a) overset(c) (int)f(x) dx + underset(c)overset(b)(int) g(x) dx`