Find the area bounded by the curves y=√1−x2 and y=x3−x without using integration.
Video Solution
Text Solution
We have y=√1−x2 (i)
and y=x3−x=x(x−1)(x+1) (ii)
Graph of (i) is the semicircle x2+y2=1 , above the x-axis.
Equation (ii) is an odd function and the graph is symmetrical about (0, 0) , intersecting the x-axis at x=0,±1.
The graphs of (i) and (ii) are as shown in the following figure.
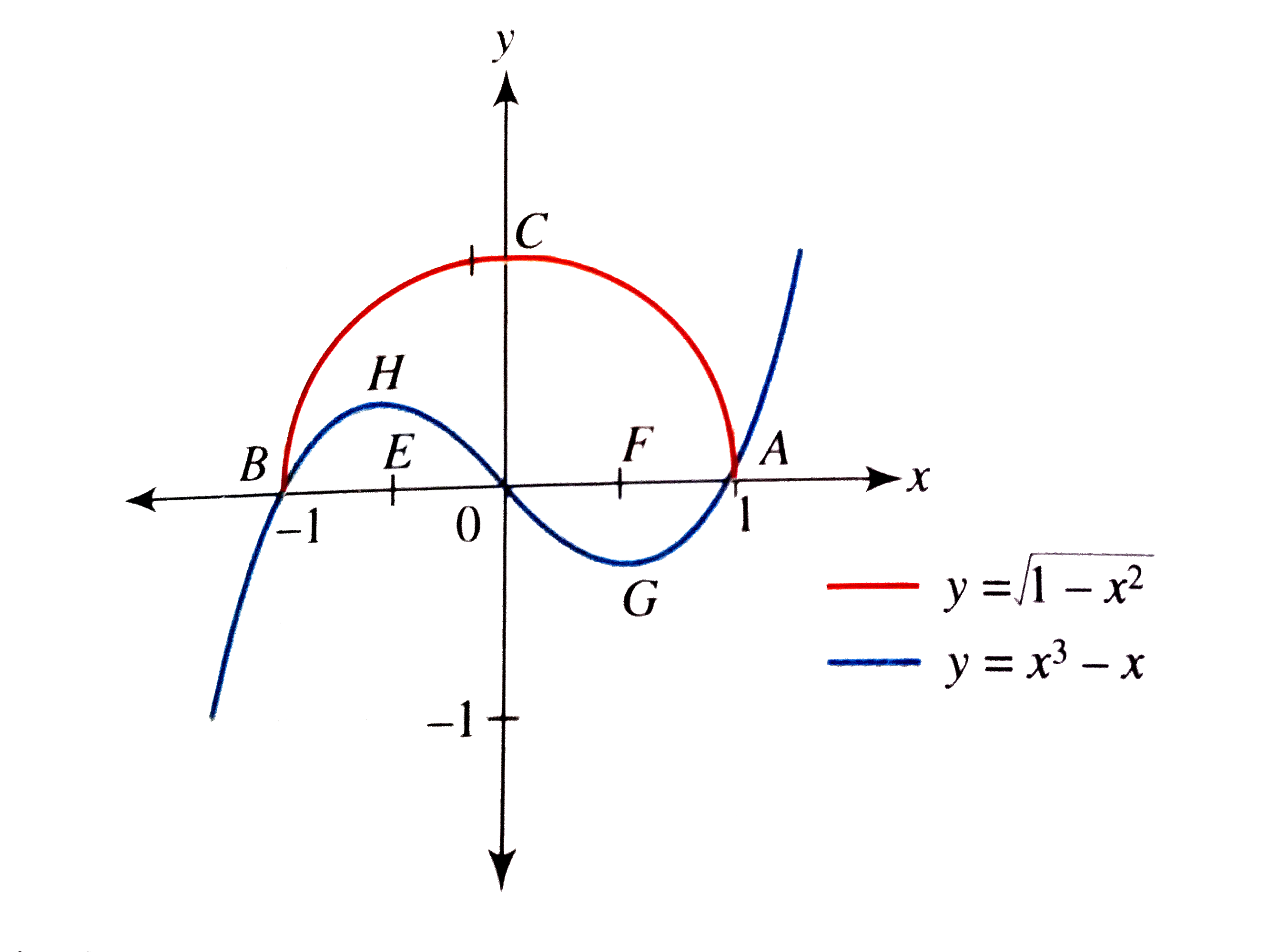
Required area, A = Area of region BHOGACB
Now Area of region BEOHB = Area of region OGAFO
Hence A = Area of of semicircle
=π/2 sq. units
|
Topper's Solved these Questions
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBook:CENGAGEChapter:GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSExercise:Exercise
Explore 13 Videos
- GRAPHICAL TRANSFORMATIONSBook:CENGAGEChapter:GRAPHICAL TRANSFORMATIONSExercise:Exercise
Explore 22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGEChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:Exercise
Explore 34 Videos
Similar Questions
Knowledge Check
Find the area bounded by the curve y√1−x2=x2
Aπ6 sq. unitsBπ4 sq. unitsCπ3 sq. unitsDπ2 sq. units
If A is the area bounded by the curves y=√1−x2 and y=x3−x , then of πA.
View SolutionFind the area bounded by the curves y=x and y=x3
View SolutionFind area bounded by curves y=√2−x2 and y = |x|.
View SolutionFind the area bounded by the curves y=√x,2y+3=x and x-axis.
View SolutionFind the area bounded by the curves y=x3−xandy=x2+x.
View Solutionfind the area bounded by the curves y=x2+1 and x+y=3
View SolutionFind the area bounded by the curves x+2|y|=1 and x=0 .
View Solution

