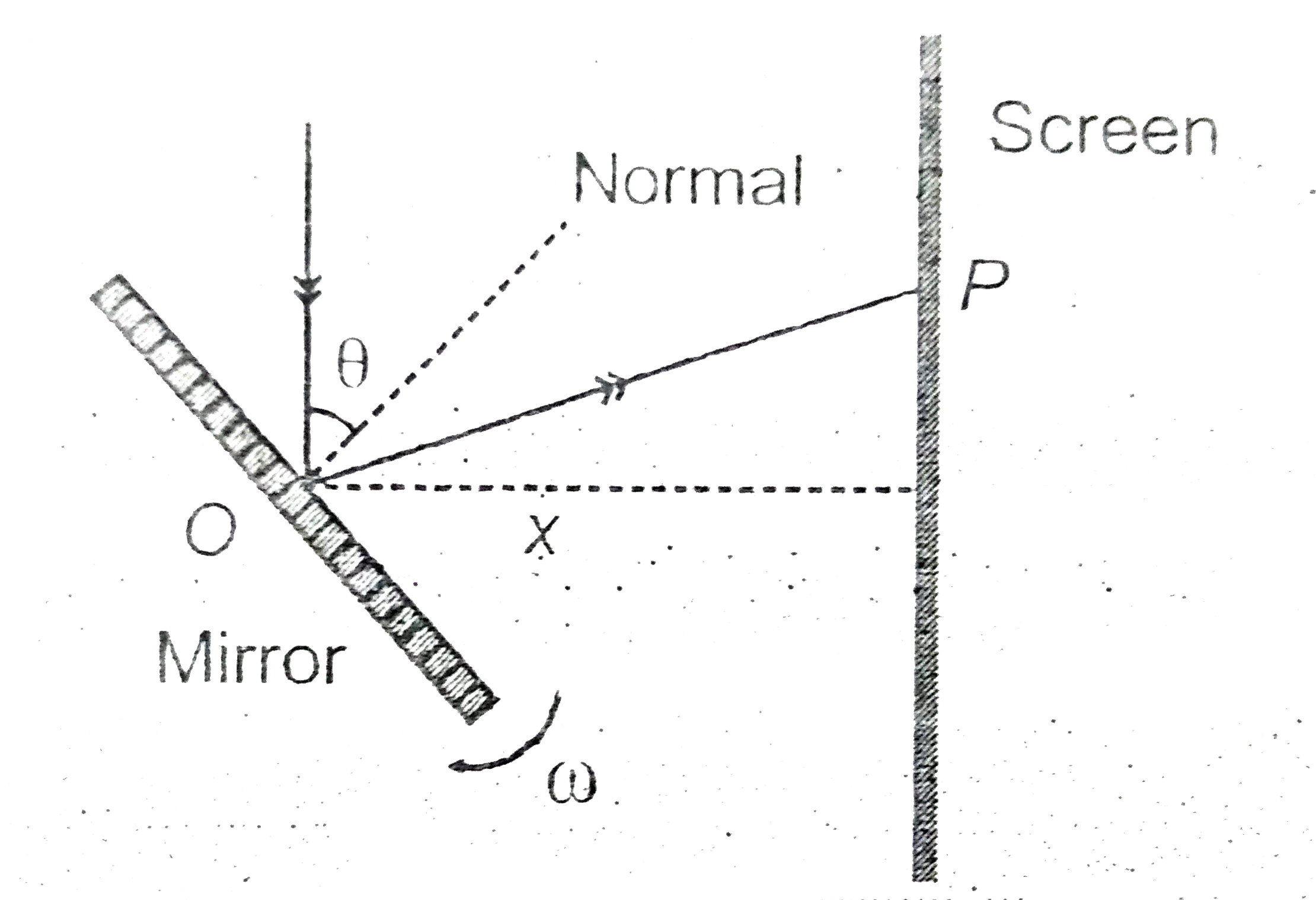
Figure shows a plane mirror hinged at O and free to rotate in a vertical plane. The point O is at a distance x from a long screen. A beam of light moving vertically downwards is reflected by the mirror at O so that a bright spot P is formed at the screen. At the instant shown, the angle of incidence is θ and the mirror is rotating clockwise with constant angular veloity ω. Find the speed of spot P at this instant.
Various angles are shown in the figure.
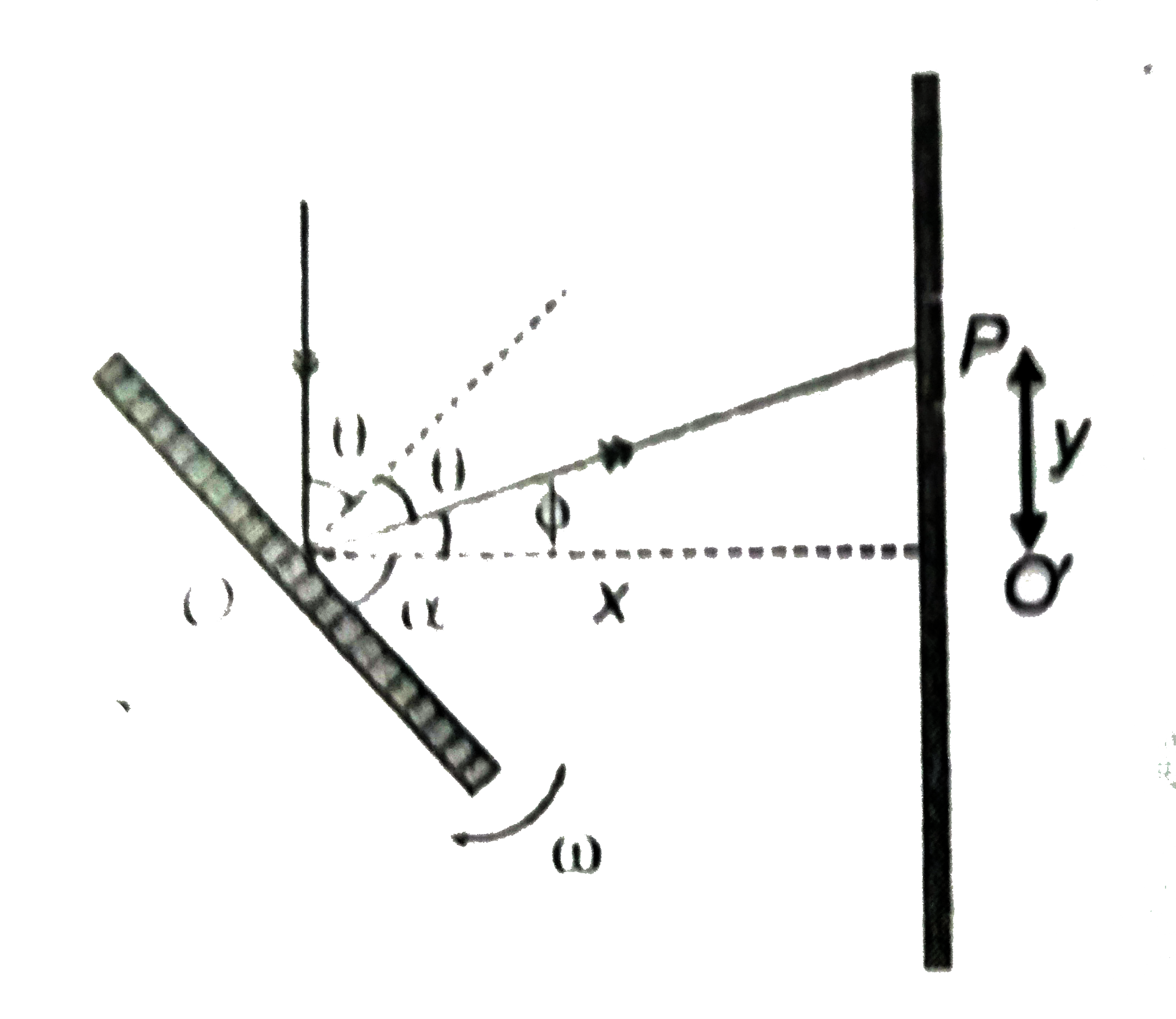
The distance of point P from O' is y at this instant.
You are supposed to calculate dydt.
From the figure,
θ+θ+ϕ=90∘ ....(i)
θ+ϕ+α=90∘ ...(ii)
⇒α=θ
⇒ϕ=2θ=90∘
or ϕ+2α=90∘
dϕdt+2dαdt=0
⇒dϕdt=−2dαdt
Note : This shows that angular speed of reflected ray is double that of mirror.
Now, y=xtanϕ
⇒dydt=xsec2φdφdt
⇒dydt=−xsec2φ×2ω
Speed =∣∣∣dydt∣∣∣=+2x(sec2ϕ)ω
Similar Questions
A small plane mirror is rotating at constant frequency of n rotations per second. With what linear velocity (in ms-1) will a light spot move along a spherical screen of radius of curvature of R metres if the mirror is at the centre of curvature of the screen?
View SolutionBy what angle the mirror must be rotated such that the reflected ray becomes vertical. Let the light ray incident on the plane mirror with an angle of incidence theta with respect to horizontal
View Solution
Knowledge Check
A plane mirror reflects a beam of light to from a real image. The incident beam is
AparallelBconvergentCdivergentDany one of the aboveIf the reflected ray is rotated by an angle of 4θ in clockwise direction then the mirror was rotated by
A2θ in anti-clockwise directionB4θ in anti-clockwise directionC2θ in clockwise directionD4θ in clockwise directionA plane mirror reflects a beam of light to form a real image, The incident beam should be
AparallelBconvergentCdivergentDnot possible
A ray of light is incident on a plane mirror placed horizontally. When the mirror is rotated through an angle 30∘ the reflected ray is found to be directed along the vertical. Determine the angle of incidence at the initial position of the mirror.
View SolutionA beam of light converges to a point on a screen S. A mirror is placed in front of the screen at a distance of 10cm form the screen. It is found that the beam now converges at a point 20cm in front of the mirror. Find the focal length of the mirror.
View SolutionA plane mirror reflects a pencil of light to form a real image. Then the pencil of light incident on the mirror is
View SolutionA plane mirror, reflecting a ray of incident light, is rotated through an angle θ about an axis through the point of incidence in the plane of the mirror perpendicular to the plane of incidence, then
View SolutionA plane mirror, reflecting a ray of incident light, is rotated through an angle θ about an axis through the point of incidence in the plane of the mirror perpendicular to the plane of incidence, then
View Solution