For a process, relation between temperature and volume is TV3=constant. If a monoatomic gas follows this process, find molar specific heat for this process
7R6
R3
11R6
Zero
The correct Answer is:A
To find the molar specific heat for the process where the relation between temperature (T) and volume (V) is given by TV3=constant, we will follow these steps:
Step 1: Express the relationship mathematically
Given the relationship TV3=C (where C is a constant), we can express temperature in terms of volume:
T=CV3
Step 2: Use the first law of thermodynamics
The first law of thermodynamics states:
dQ=dU+dW
where dQ is the heat added, dU is the change in internal energy, and dW is the work done by the system.
Step 3: Calculate the change in internal energy (dU)
For a monoatomic ideal gas, the change in internal energy is given by:
dU=nCVdT
where CV=32R for a monoatomic gas.
Step 4: Calculate the work done (dW)
The work done by the gas during an infinitesimal expansion is given by:
dW=PdV
Using the ideal gas law, PV=nRT, we can substitute for P:
P=nRTV
Substituting T from our earlier expression:
P=nR(CV3)V=nRCV4
Thus, the work done becomes:
dW=nRCV4dV
Step 5: Substitute dU and dW into the first law
Now substituting dU and dW into the first law:
dQ=nCVdT+dW
Substituting for dW:
dQ=nCVdT+nRCV4dV
Step 6: Find dT in terms of dV
From T=CV3, we differentiate:
dT=−3CV4dV
Step 7: Substitute dT into the heat equation
Substituting dT into the equation for dQ:
dQ=nCV(−3CV4dV)+nRCV4dV
dQ=(−3nCV+nR)CV4dV
Step 8: Identify the molar specific heat (C)
The molar specific heat C for the process can be defined as:
C=dQdT
Using the relationship from above, we can express C in terms of n:
C=−3CV+R
Substituting CV=32R:
C=−3(32R)+R=−92R+R=−72R
Step 9: Final result
Thus, the molar specific heat for the process is:
C=−72R
Given the relationship TV3=C (where C is a constant), we can express temperature in terms of volume:
T=CV3
The first law of thermodynamics states:
dQ=dU+dW
where dQ is the heat added, dU is the change in internal energy, and dW is the work done by the system.
For a monoatomic ideal gas, the change in internal energy is given by:
dU=nCVdT
where CV=32R for a monoatomic gas.
The work done by the gas during an infinitesimal expansion is given by:
dW=PdV
Using the ideal gas law, PV=nRT, we can substitute for P:
P=nRTV
Substituting T from our earlier expression:
P=nR(CV3)V=nRCV4
Thus, the work done becomes:
dW=nRCV4dV
Now substituting dU and dW into the first law:
dQ=nCVdT+dW
Substituting for dW:
dQ=nCVdT+nRCV4dV
From T=CV3, we differentiate:
dT=−3CV4dV
Substituting dT into the equation for dQ:
dQ=nCV(−3CV4dV)+nRCV4dV
dQ=(−3nCV+nR)CV4dV
The molar specific heat C for the process can be defined as:
C=dQdT
Using the relationship from above, we can express C in terms of n:
C=−3CV+R
Substituting CV=32R:
C=−3(32R)+R=−92R+R=−72R
Thus, the molar specific heat for the process is:
C=−72R
Topper's Solved these Questions
- THERMODYNAMICSBook:AAKASH INSTITUTEChapter:THERMODYNAMICSExercise:Assignment (Section-C) Objective Type Questions (More than one option are correct)
Explore 11 Videos
- THERMODYNAMICSBook:AAKASH INSTITUTEChapter:THERMODYNAMICSExercise:Assignment (Section-D) Linked comprehension Type questions
Explore 3 Videos
- THERMODYNAMICSBook:AAKASH INSTITUTEChapter:THERMODYNAMICSExercise:Assignment (Section-A) Objective Type Questions (one option is correct)
Explore 50 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH INSTITUTEChapter:THERMAL PROPERTIES OF MATTERExercise:Assignment (Section-J) Akash Challengers Questions
Explore 7 Videos
- UNITS AND MEASUREMENTSBook:AAKASH INSTITUTEChapter:UNITS AND MEASUREMENTSExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
Similar Questions
One mole of a monoatomic ideal gas undergoes the process A→B in the given P-V diagram. What is the specific heat for this process?
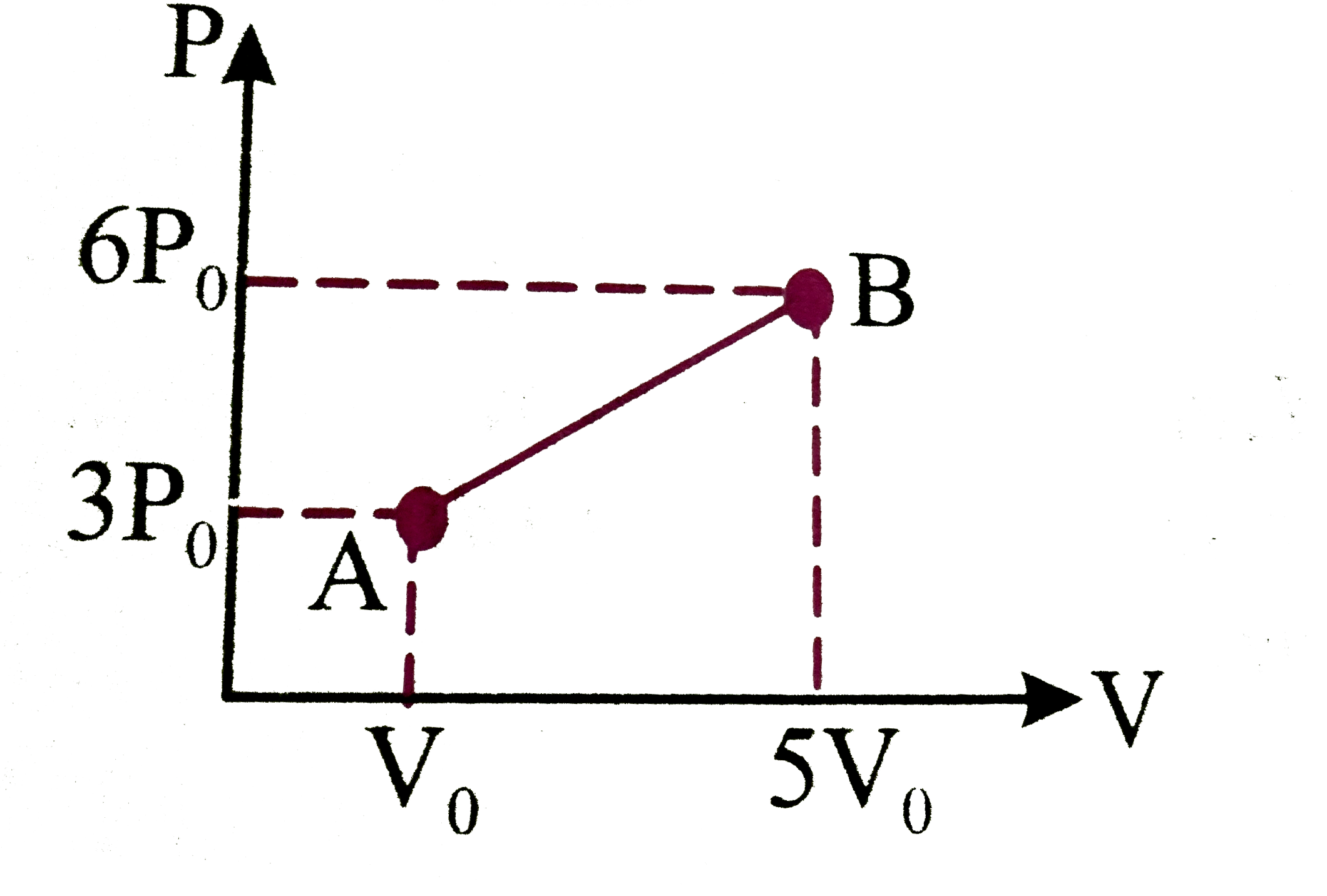
View SolutionIn a process, temperature and volume of one mole of an ideal monoatomic gas are varied according to the relation VT= K, where K is a constant. In this process the temperataure of the gas is increased by ΔT. The amount of heat absorbed by gas is (R is gas constant).
View Solution
Knowledge Check
One mole of a monoatomic ideal gas undergoes process AB in given P – V diagram then average specific heat for this process is:
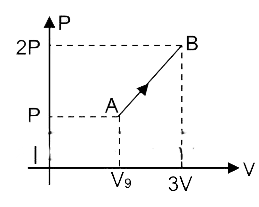 A21R10B18R10C9R10D13R10
A21R10B18R10C9R10D13R10A monoatomic gas undergoes a process in which the pressure (P) and the volume (V) of the gas are related as PV−3=constant. What will be the molar heat capacity of gas for this process?
A5R3B35RC75RDR4For a monoatomic ideal gas undergoing an adiabatic change, the relation between temperature and volume is TVx = constant, where x is
A7/5B2/5C2/3D1/3
An ideal gas undergoes a process in which its pressure and volume are related as PVn=constant,where n is a constant.The molar heat capacity for the gas in this process will be zero if
View SolutionOne mole of an ideal monoatomic gas undergoes a process as shown in the figure. Find the molar specific heat of the gas in the process.
R is a gas constant.
View SolutionFor a monoatomic ideal gas undergoing an adiabatic change, the relation between temperature and volume TVx = constant, where x is
View SolutionThe molar heat capacity for an ideal gas (i) Is zero for an adiabatic process
(ii) Is infinite for an isothermal process
(iii) depends only on the nature of the gas for a process in which either volume or pressure is constant
(iv) Is equal to the product of the molecular weight and specific heat capacity for any process
View SolutionAn ideal gas may expands from V0 to 2V0 according to following three processes. Molar specific heat for processes b will be

View Solution