A planet moves in elliptical around sun, at one of focal points. Match the following, for different parameters related to the planet during the motion
Column IColumn II(A)Kinetic energy(p)Maximum at perigee(B)Gravitational potential energy(q)Minimum at perigee(C)Linear momentum(r)Maximum at apogee(D)Area swept per second radius(s)Minimum at apogee
The correct Answer is:A, B, C, D
Step by step video, text & image solution for A planet moves in elliptical around sun, at one of focal points. Match the following, for different parameters related to the planet during the motion {:(,"Column I",,"Column II"),((A),"Kinetic energy",(p),"Maximum at perigee"),((B),"Gravitational potential energy",(q),"Minimum at perigee"),((C ),"Linear momentum",(r ),"Maximum at apogee"),((D),"Area swept per second radius",(s),"Minimum at apogee"):} by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -G (Integer Answer Type Questions)6videos
GRAVITATION
- BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -H (Multiple True - False Type Questions)5videos
GRAVITATION
- BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -E (Assertion - Reason Type Questions)14videos
GRAVITATION
- BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D13videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions10videos
KINETIC THEORY
Similar Questions
Match the following :
Column-1 Column-2(A)Electrostatic potential energy(P) Positive(B)Gravitational potential energy(Q) Negative(C)Elastic potential energy(R) Zero(D)Magnetic potential energy(S) Not definedView SolutionColumn IColumn II(a)Work(p)WF(b)Kinetic energy(q)mgh(c)Potential energy(r)12mv2(d)Displacement(s)F×S
View Solution
Knowledge Check
- Question 1 - Select One
Match the following columns. (for a satellite in circular orbit)
Column-IColumn-II(A)Kinetic energy(p)−GMm2r(B)Potential energy(q)√GMr(C)Total energy(r)−GMmr(D)Orbital speed(s)GMm2rA(A→s,B→r,C→p,D→q)B(A→c,B→s,C→p,D→q)C(A→s,B→r,C→q,D→p)D(A→q,B→r,C→p,D→s)
Match the following :
Column -IColumn -II(A)Acceleration due to gravity(p)Kepler's law(B)Law of periods(q)Vector quantity(C)Orbital speed(r)Uniform near earth surface(D)Gravitational potential(s)Is nearly zero at infinityView SolutionDensity of a planet is two times the density of earth. Radius of this planet is half. Match the following (as compared to earth)
Column-IColumn-II(A)Accleration due to gravity on this planet's surface(p)Half(B)Gravitational potential on the surface(q)Same(C)Gravitational potential at centre(r)Two times(D)Gravitational field strength at centre(s)Four timesView SolutionMatch the following
Column-IColumn-II(A)Enthalpy(p)Extensive property(B)Entropy(q)H - TS(C)Free energy(r)E + PV(D)Pressure(s)Intensive propertyView SolutionIn elliptical orbit of a planet, as the planet moves from apogee position to perigee position to perigee position, match the following columns
Column-IColumn-II(A)Speed of planet(p)Remains same(B)Distance of planet from centre of sun(q)Decreases(C)Potential energy(r)Increase(D)Angular momentum about centre of sun(s)Cannot sayView SolutionMatch the following
Column-IColumn-II(A)Derived unit(p)Height(B)Fundamental unit(q)Thickness(C)Derived quantity(r)Area(D)Fundamental quantity(s)Newton(t)KilogramView SolutionIf earth decreases its rotational speed. Match the following columns
Column-IColumn-II(A)Value of g at pole(p)Will remain same(B)Value of g at equator(q)Will increase(C)Distance of geostationary(r)Will decrease(D)Energy of geostationary satellite(s)Cannot sayView SolutionCurrent I is following through a wire of non-uniform cross-section as shown. Match the following columns.
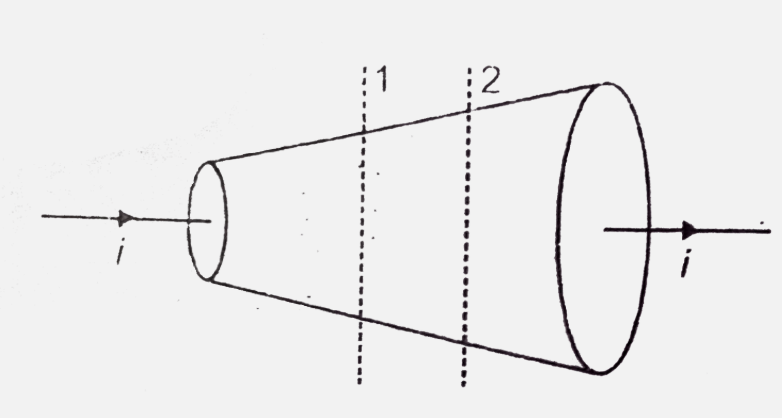
Column IColumn II(A)Current density(p)More at section 1 than 2(B)Electric field(q)More at section 2 than 1(C)Resistance per unit length(r)Same at both section 1 and 2 (D)Potential difference per unit length(s)Data insufficientView Solution

