A force F is applied on a disc at it's centre. Find acceleration of center of mass in the case of pure rolling and also find minimum coefficient of fricition required for pure rolling.
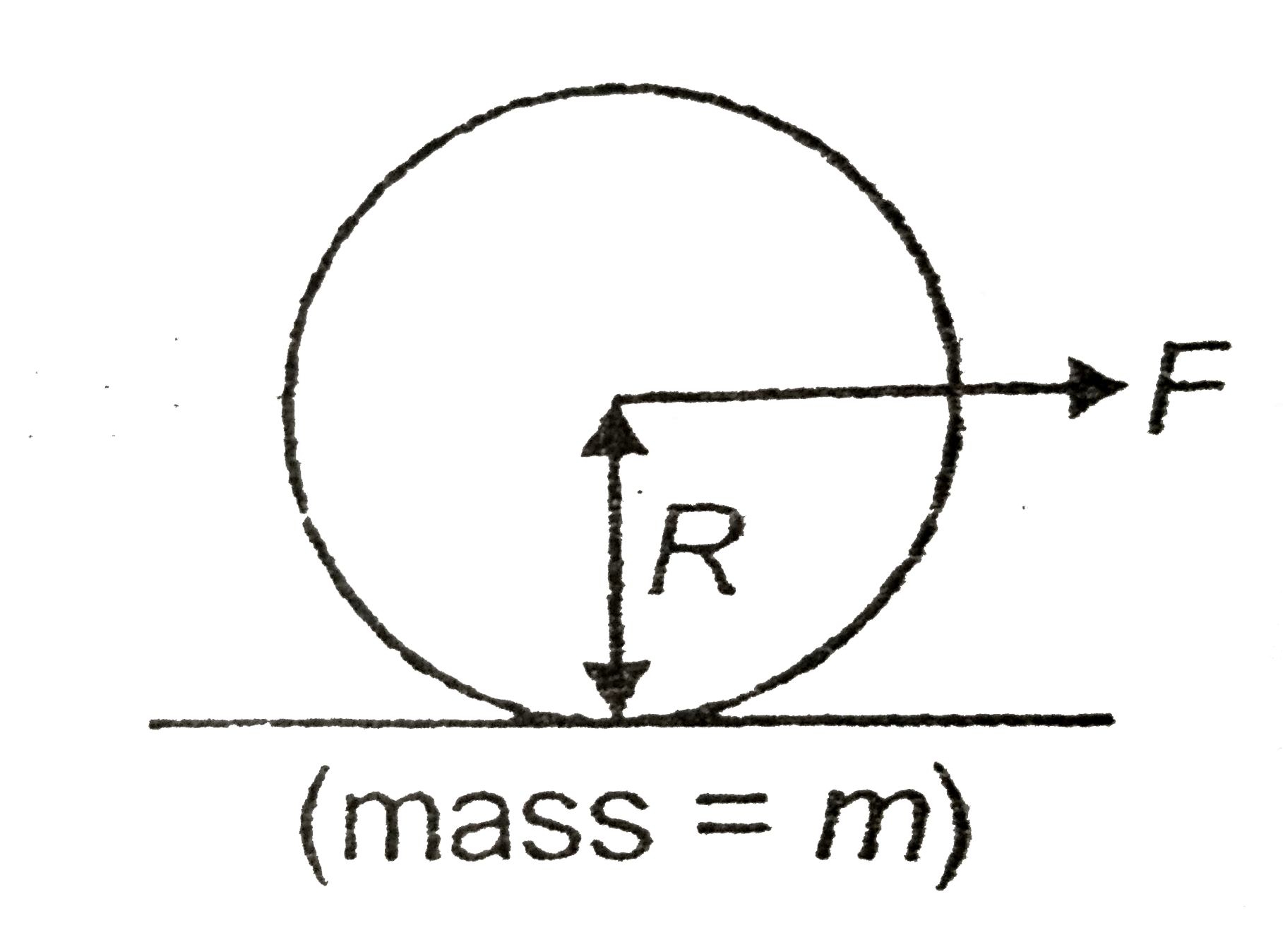

Let the friction force acting on disc be fr, acceleration of centre of mass is a and angular acceleration is α.
We have three unknowns
(i) a
(ii)α
(iii)fr
We require 3 equations to solve them
Translatory Motion
F−fr=ma......(i)
Rotatory Motion
r⋅fr=mr22⋅α........(ii)
Condition of no slipping
a=rα..........(iii)
By solving (ii) & (iii)
fr=ma2, F=3ma2⇒a=2F3m, fr=m2×2F3m, fr=F3
Now, fr≤μN
⇒F3≤μmg
⇒μ≥F3mg
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTEChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Illustration
Explore 4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTEChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Assignment (Section - A) Objective Type Questions (One option is correct)
Explore 62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:AAKASH INSTITUTEChapter:SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:Assignment (Section-D (Assertion and reason))
Explore 5 Videos
- TEST 1Book:AAKASH INSTITUTEChapter:TEST 1Exercise:EXERCISE
Explore 9 Videos
Similar Questions
Derive an expression for the acceleration of a solid cylinder rolling without slipping down an inclined plane. Also find the minimum coefficient of friction required for pure rolling
View SolutionIf a solid cylinder rolls without slipping on an inclined plane of inclination 45°, then the minimum coefficient of friction required to support pure rolling is
View Solution
Knowledge Check
A force F is applied horizontally on a cylinder in the line of centre as shown in the figure. The cylinder is on a rough surface of coefficient of fricition μ. The direction of the friction force acting on the cylinder will be
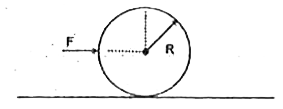 Ain the direction of FBzeroCin opposite direction of FDcan not be ascertained
Ain the direction of FBzeroCin opposite direction of FDcan not be ascertained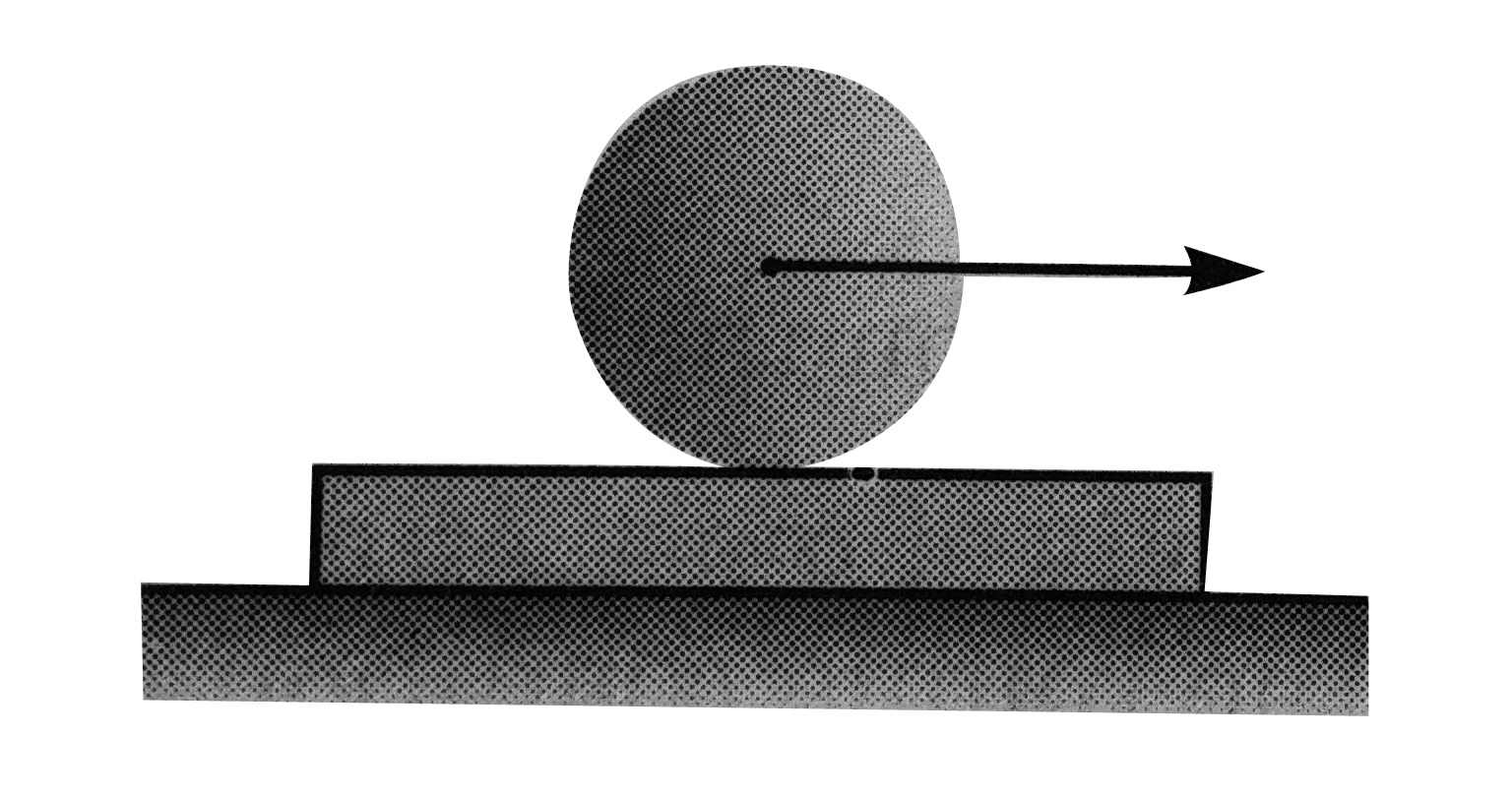
A horizontal force F is applied at the centre of solid sphere placed over a plank. The minimum coefficient of friction between plank and sphere required for pure rolling is μ1 when plank is kept at rest ad μ2 when plank can move, then μ2<μ1
Reason: Work done by frictional force on the sphere in both cases is zero.AIf both Assertion and Reason are true and the Reason is correct explanation of the Assertion.BIf both Assertion and Reason are true but Reason is not the correct explanation of Assertion.CIf assertion is true, but the reaction is false.DIf assertion is false but the reason is true.A force F is applied at the centre of a disc of mass M. The minimum value of coefficient of friction of the surface for rolling is
AF2MgBF3MgC2F5MgD2F7Mg
If a solid cylinder rolls without slipping on an inclined plane of inclination 45° then the minimum coefficient of friction required to support pure rolling is
View SolutionA sphere of mass m rols wilthout sliping on an inclined plane of inclination θ. Find the linear acceleration o the sphere and the force of friction acting on it. What should be the minimum coefficient o static friction to support pure rolling?
View SolutionA cylinder of mass m rolls without slipping on an inclined plane of inclination θ. Find the liner acceleration of the sphere and friction acting on it. What should be the minimum coefficient of static friction to support pure rolling?
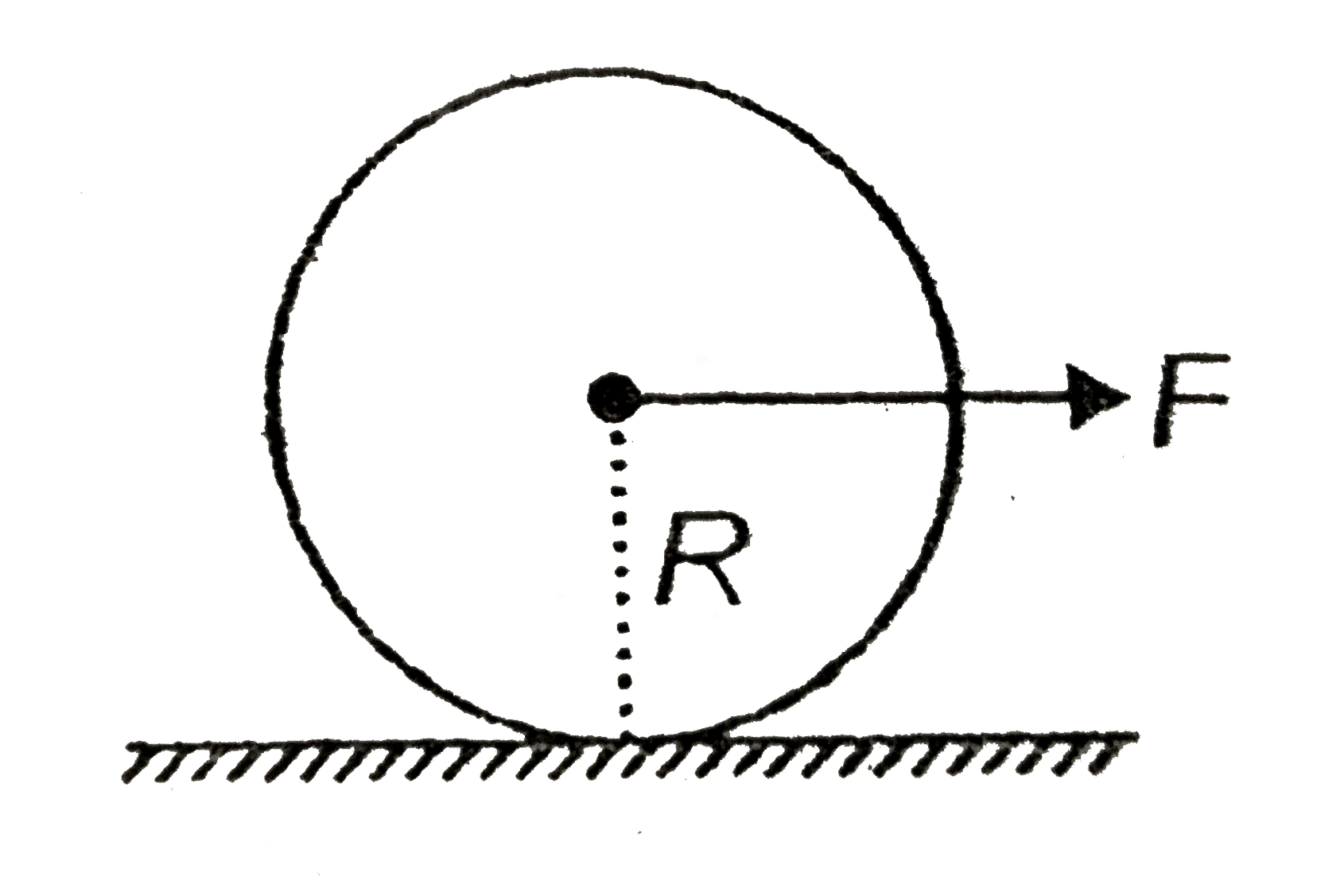
View SolutionA force F is applied at center of a uniform round object of mass m radius R and moment of inertia about its centre of mass Icm. Find (if IcmmR2=k).
(a) Acceleration of center of the round object if it rolls without slipping.
(b) Minimum coefficient of fricition required so that the round object rolls without slipping.
View SolutionA uniform solid disk rolling down an incline making angle θ with the horizontal. The minimum coefficient of friction required to maintain pure rolling motion for the disk is.
View Solution

