A cylinder of mass $m$ rolls without slipping on an inclined plane of inclination $θ$ . Find the liner acceleration of the sphere and friction acting on it. What should be the minimum coefficient of static friction to support pure rolling?

Video Solution

Text Solution

Verified by Experts

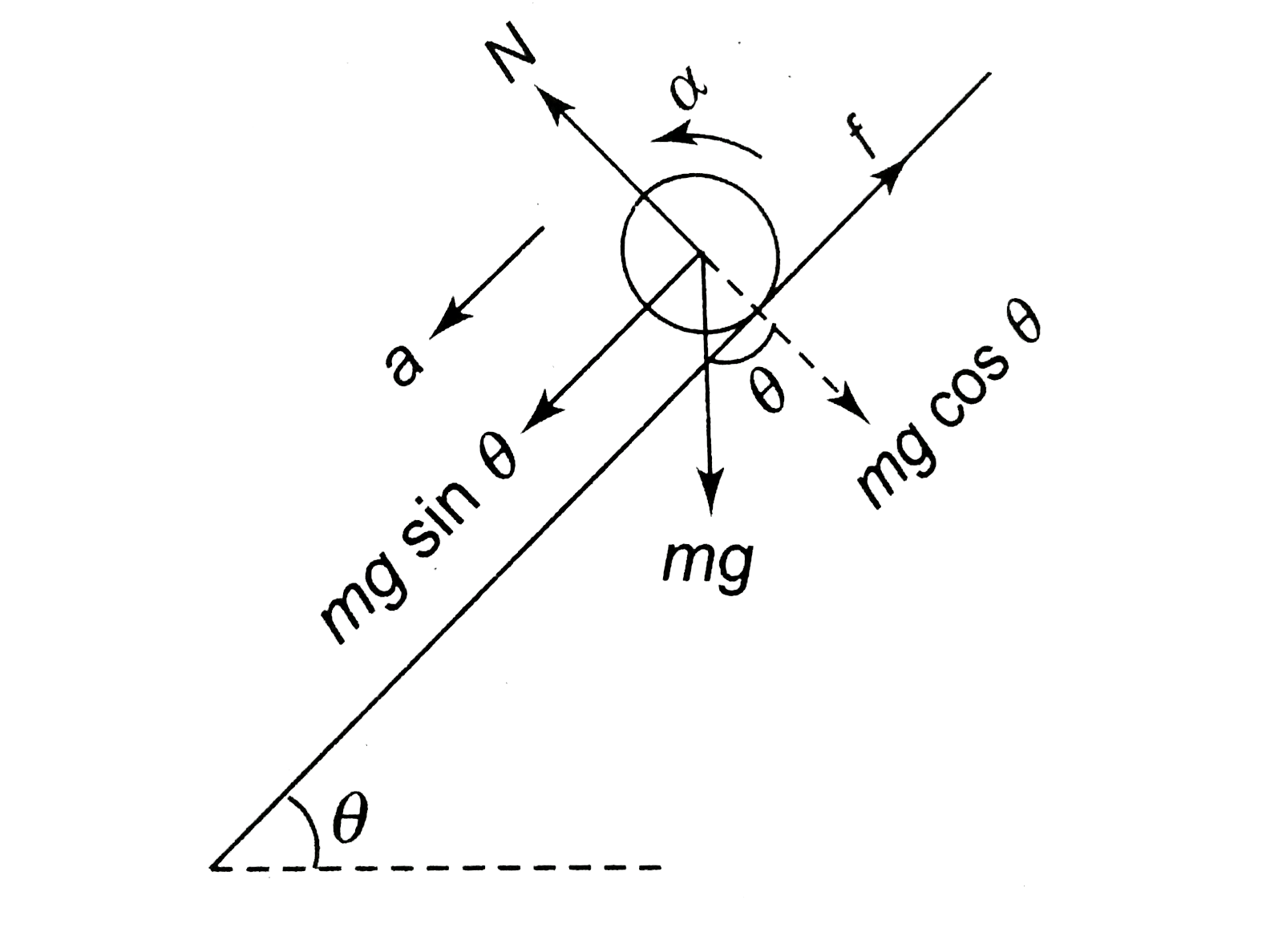
Linear motion: $m g sin θ - f = m a$ ( $i$ )
Rotational motion: $f R = I α = (\frac{1}{2} m r^{2}) (\frac{a}{r})$
$f = \frac{1}{2} m a$ ( $i i$ )
(for pure rolling $a = r α$ )
From ( $i$ ) and ( $i i$ )
$m g sin θ - \frac{1}{2} m a = m a$
$m g sin θ = \frac{3}{2} m a \Rightarrow a = \frac{2}{3} g sin θ$
$f = \frac{1}{2} m a = \frac{1}{3} m g sin θ$
$f_{max} = μ N = μ m g cos θ :$ coefficient of static friction.
For pure rolling $f_{max} \geq f$
$μ m g cos θ \geq \frac{1}{3} m g sin θ \Rightarrow μ \geq \frac{1}{3} tan θ$
$μ_{min} = \frac{1}{3} tan θ$
OR
In pure rolling
$a = \frac{g sin θ}{1 + k^{2} / R^{2}} = \frac{g sin θ}{1 + \frac{1}{2}} = \frac{2}{3} g sin θ$
$m g sin θ - f = m a \Rightarrow f = \frac{1}{3} m g sin θ$
$μ \geq \frac{tan θ}{1 + \frac{R^{2}}{k^{2}}}$
$μ_{min} = \frac{tan θ}{1 + 2} = \frac{1}{3} tan θ$

Updated on:21/07/2023

A solid sphere of mass m rolls without slipping on an inclined plane of inclination $θ$ . The linear acceleration of the sphere is
A $\frac{7}{5} g sin θ$
B $\frac{2}{7} g sin θ$
C $\frac{3}{7} g sin θ$
D $\frac{5}{7} g sin θ$
A sphere rolls down on an inclied plane of inclination $θ$ . What is the acceleration as the sphere reaches bottom ?
A $\frac{5}{7} g sin θ$
B $\frac{3}{5} g sin θ$
C $\frac{2}{7} g sin θ$
D $\frac{2}{5} g sin θ$
Acceleration of a solid cylinder rolling without slipping down an incline of inclination $θ$ is
A $\frac{2}{3} g sin θ$
B $\frac{2}{3} g cos θ$
C $\frac{2}{3} g$
D $\frac{2}{3} g tan θ$