The position of a particle moving on a stringht line under rthe action of a force is given as Here, x is in metre and t is in second. If mass of the particle is 2 kg, the work done by the force acting on the particle in first 5 s is.
2500 J
5000 J
The correct Answer is:B
Step by step video, text & image solution for The position of a particle moving on a stringht line under rthe action of a force is given as x=50t-5t^(2) Here, x is in metre and t is in second. If mass of the particle is 2 kg, the work done by the force acting on the particle in first 5 s is. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:SECTION-C (OBJECTIVE TYPE QUESTIONS) (MORE THAN ONE OPTIONS ARE CORRECT)
Explore 16 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:SECTION-D (LINKED COMPREHENSION TYPE QUESTIONS) (COMPREHENSION-I)
Explore 3 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:SECTION-A (OBJECTIVE TYPE QUESTIONS (ONE OPTIONISCORRECT)
Explore 60 Videos
- WAVESBook:AAKASH INSTITUTEChapter:WAVESExercise:ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
Explore 12 Videos
Similar Questions
Under the action of a force, a 3 kg body moves such that x=t22, where position x is in metre and t is in second. What is the work done by the force in first 3 second?
View SolutionThe position of a Particle of Mass 4 g,acted upon by a constant force is given by x=4t2+t,where x is in metre and t in second .The work done during the first 2 seconds is
View Solution
Knowledge Check
The position of a particle moving in a straight line is given by
x=3t3−18t2+36t
Here, x is in m and t in second. ThenAdirection of velocity and acceleration both change at t=2sBthe distance travelled by particle is equal to magnitude of displacement for t=0 to t=5sCthe speed of particle is decreasing in t=0 to t=2s then it is increasing for t>2DThe magnitudes of velocity and acceleration are equal at t=0Force acting on a particle is given by F=A−xBt, where x is in metre and t is in seconds. The dimensions of B is -
AMLT−2BM−1T−3CM−1TDMT−1The position of a particle moving in a string line is given by
x=3t3−18t2+36t
Here, x is in m and t in second . ThenAdirection of velocity and acceleration both change at t=2sBthe distance travelled by particle is equal to magnitude of displacement, for t=0 to t=5sCthe speed of particle is decreasing in t=0 to t=2s then it is increasing for t>2Dthe magnitudes of velocity and acceleration are equal at t=0
The displacement of a particle moving in a straight line is described by the relation s=6+12t−2t2. Here s is in metre and t in second. The distance covered by the particle in first 5s is
View SolutionThe position of a particle is given by
x=2(t−t2)
where t is expressed in seconds and x is in metre.
The particle
View SolutionVelocity-time graph of a particle moving in a straight line is shown in the figure. Mass of the particle is 2 kg. Work done by all the forces acting on the particle in time interval t = 0 to t = 10 sec is
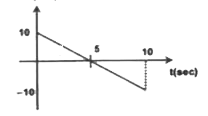
View SolutionThe displacement of a particle moving in a straight line, is given by s=2t2+2t+4 where s is in metres and t in seconds. The acceleration of the particle is.
View SolutionThe velocity-time graph of a particle moving in a straight line is shown in figure. The mass of the particle is 2kg. Work done by all the forces acting on the particle in time interval between t=0 to t=10s is

View Solution

