A bullet of mass m hits a block of mass M. The transfer of energy is maximum when
m>>M
M>>m
M=2m
M=m
The correct Answer is:D
To solve the problem of when the transfer of energy is maximum when a bullet of mass m hits a block of mass M, we can analyze the situation using the principles of conservation of momentum and kinetic energy.
1. Understand the Scenario:
- A bullet of mass m is moving with an initial velocity v and strikes a block of mass M. We need to determine the condition under which the transfer of kinetic energy from the bullet to the block is maximized.
2. Conservation of Momentum:
- According to the law of conservation of momentum, the total momentum before the collision must equal the total momentum after the collision.
- The equation can be expressed as:
mv=mv1+MVf
where v1 is the velocity of the bullet after the collision, and Vf is the velocity of the block after the collision.
3. Kinetic Energy Before Collision:
- The initial kinetic energy of the bullet is given by:
KEinitial=12mv2
4. Kinetic Energy After Collision:
- The kinetic energy after the collision can be expressed as:
KEfinal=12mv21+12MV2f
5. Condition for Maximum Energy Transfer:
- The maximum transfer of energy occurs when the bullet comes to rest after the collision, meaning v1=0. Under this condition, all the kinetic energy of the bullet is transferred to the block.
- Therefore, the kinetic energy transferred to the block is:
KEtransferred=12MV2f
6. Setting Up the Equation:
- From the conservation of momentum, if the bullet comes to rest, we have:
mv=MVf
- Rearranging gives:
Vf=mvM
7. Substituting into Kinetic Energy:
- Substitute Vf into the kinetic energy equation:
KEtransferred=12M(mvM)2=12m2v2M
8. Maximizing Energy Transfer:
- To maximize the transferred energy, we need to consider the ratio of the masses. The maximum energy transfer occurs when the mass of the block M is equal to the mass of the bullet m:
M=m
Conclusion:
The transfer of energy is maximum when the mass of the block is equal to the mass of the bullet, i.e., M=m.
- A bullet of mass m is moving with an initial velocity v and strikes a block of mass M. We need to determine the condition under which the transfer of kinetic energy from the bullet to the block is maximized.
- According to the law of conservation of momentum, the total momentum before the collision must equal the total momentum after the collision.
- The equation can be expressed as:
mv=mv1+MVf
where v1 is the velocity of the bullet after the collision, and Vf is the velocity of the block after the collision.
- The initial kinetic energy of the bullet is given by:
KEinitial=12mv2
- The kinetic energy after the collision can be expressed as:
KEfinal=12mv21+12MV2f
- The maximum transfer of energy occurs when the bullet comes to rest after the collision, meaning v1=0. Under this condition, all the kinetic energy of the bullet is transferred to the block.
- Therefore, the kinetic energy transferred to the block is:
KEtransferred=12MV2f
- From the conservation of momentum, if the bullet comes to rest, we have:
mv=MVf
- Rearranging gives:
Vf=mvM
- Substitute Vf into the kinetic energy equation:
KEtransferred=12M(mvM)2=12m2v2M
- To maximize the transferred energy, we need to consider the ratio of the masses. The maximum energy transfer occurs when the mass of the block M is equal to the mass of the bullet m:
M=m
The transfer of energy is maximum when the mass of the block is equal to the mass of the bullet, i.e., M=m.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:SECTION-B (SUBJECTIVE TYPE QUESTIONS) (ONE OPTIONS IS CORRECT)
Explore 44 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:SECTION-C (OBJECTIVE TYPE QUESTIONS) (MORE THAN ONE OPTIONS ARE CORRECT)
Explore 16 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:TRY YOURSELF
Explore 95 Videos
- WAVESBook:AAKASH INSTITUTEChapter:WAVESExercise:ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
Explore 12 Videos
Similar Questions
A bullet of mass m strikes a block of mass M. The bullet remains embedded in the block. Find the amplitude of the resulting SHM.

View SolutionA bullet of mass m strikes a block of mass M connected to a light spring of stiffness k, with a speed v0 and gets into it. Find the loss of K.E. of the bullet.

View Solution
Knowledge Check
A bullet of mass m is fired into a block of wood of mass M which hangs on the end of pendulum and gets embedded into it. When the bullet strikes with maximum rise R. Then, the velocity of the bullet is given by
AMm+M(√2gRBM+mm√2gRC(Mm)√2gRDNone of theseIn a free space a rifle on mass M shoots a bullet of mass m at a stationary block of mass M distance D away from it . When the bullet has moved through a distance d towards the block the centre of mass of the bullet − block system is at a distance of :
A(D−d)mM+m from the blockBmd+MDM+m from the rifleC2dm+DMM+m from the rifleD(D−d)=MM+m from the bulletA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
A12mv2×m(m+M)B12mv2×M(m+M)C12mv2×(M+m)mD12Mv2×m(m+M)
A bullet of mass m strikes a block of mass M connected to a light spring of stiffness k, with a speed v0 and gets into it. Find the loss of K.E. of the bullet.
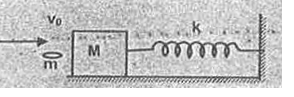
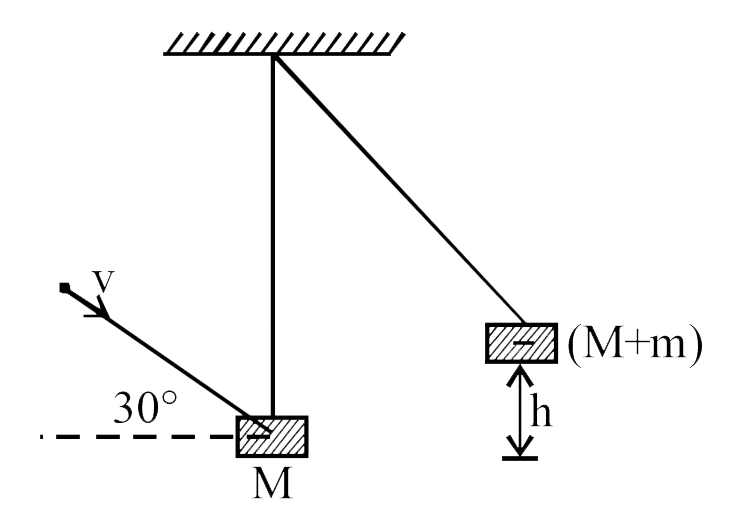
View SolutionA bullet of mass 20 g hits a block of mass 1.98 kg suspended from a massless string of length 100 cm and sticks to it. The bullet flies down at an angle of 30º to the horizontal with a velocity of 200 m/s. Through what height the block will rise-
View SolutionA bullted of mass m embeds itself in a block of mass M resting on a smooth horizontal surface, attached to a spring of force constant k. If the initial sped of the bullet is v0 along horizontal, find (a) the maximum compression of the spring and (b) the time forthe bullet - block system to come to rest.
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA bullet of mass m hits a target of mass M hanging by a string and gets embeded in it. If the block rises to a height h as a result of this collision, the velocity of the bullet before collision is
View Solution

