An object is thrown vertically upward with some speed. It crosses 2 points p,q whith are separated by (h) metre. If (t) is the time between (p) and highest point and coming back and tq is the time between q and highest point and coming back, relate acceleration due to gravity tp,tqandh.
Strategy: Let u' be velocity of the object while crossing point a and v' be its velocity while crossing point b. As shown P is the highest point of vertical motion of object. The time taken by the object in going a to P=ta/2 the time taken by the object in going from b to P=t02
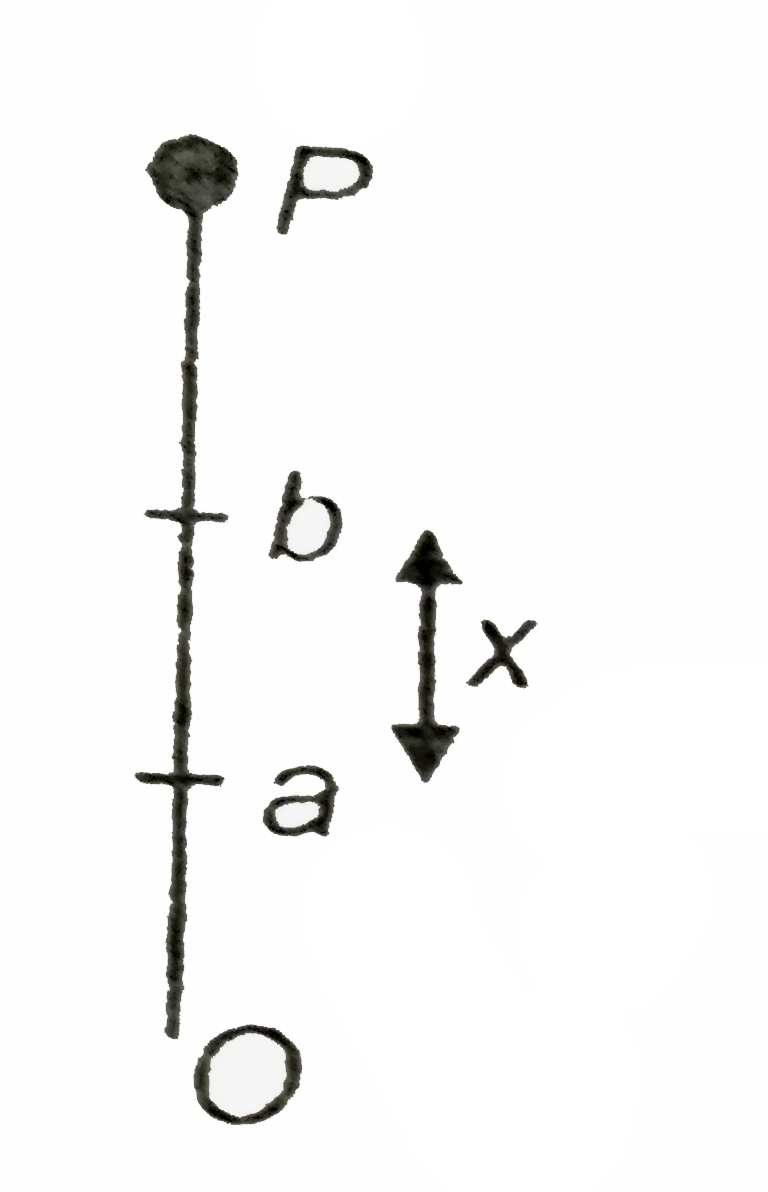
Taking vertical upward motion of object from a to P we have
u=v',v=0,a=−g,t=ta2
As, v=u+at
∴ 0=u'+(−g)ta2 or u'=gta2 ...(i)
Taking vertical upward motion of object from b to P, we have
u=v',v=0,a=−g,t=tb2
As, v=u+at
0=v'(−g)tb2 or v'=gtb2 ...(ii)
Taking vertical upward motion of object from a to b, we have
u=u',v=v',a=−g,s=x
As, v2=u2+2as
∴ v'2=u'2+2(−g)(x)
or 2gx=u'2−v'2=g2t2a4−g2t2b4
2gx=g24[t2a−t2b]
x=g8[t2a−t2b]
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Try Yourself
40 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - A)
50 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTECHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTECHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
Similar Questions
Normals drawn to the hyperbola xy=2 at the point P(t1) meets the hyperbola again at Q(t2), then minimum distance between the point P and Q is
View SolutionA car starts from a point P at time t = 0 seconds and stops at point Q. The distance x, in metres, covered by it, in t seconds is given by x=t2(2−t3)Find the time taken by it to reach Q and also find distance between P and Q.
View Solution
Knowledge Check
From a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is
AgH = (n−2)u2B2 gH = n2u2CgH = (n−2)2u2D2 gH = ν2(n−2)A particle is thrown vertically upwards from the surface of the earth. Let TP be the time taken by the particle to travel from a point P above the earth to its highest point and back to the point P. Similarly, let TQ be the time taken by the particle to travel from another point Q above the earth to its highest point and back to the same in terms of TP,TQ and H, is :-
A6HT2P+T2QB8HT2P+T2QC2HT2P+T2QDHT2P+T2QA particle is projected vertically from the ground, takes time t1 upto point A, t2 from point A to B and time t3 from point B to highest point and back to the ground. Find the height of the middle point of A and B from the ground.
Ag2[t21+t22+2(t1t2+t2t3+t3t1)]Bg4[t212+t222+t1t2+t1T3+t2t3]Cg2[t21+t22+t1t2+t1t3+t2t3]Dnone of the above
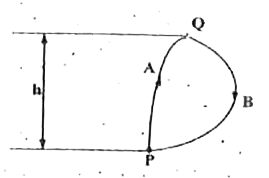
A particle is taken from point P to point Q via the path PAQ and then placed back to point P via the path QBP. Find the work done by gravity on the body over this closed path. Vertical separation between P and Q is h as shown.
View SolutionIn the following displacement (x) vs time (t) graph, at which among the point P,Q and R is the object speed increasing ?

View SolutionThe reation between the time t and position x for a particle moving on x-axis is given by t=px2+qx, where p and q are constants. The relation between velocity v and acceleration a is as
View SolutionP is the father of Q and R is the son of S. T is the brother of P. Q is the sister of R. How is S related to T?
View SolutionIn following displacement (x) vs time (t) graph at which among the P,Q and R is the object's speed increasing ?

View Solution
