Starting with the thermodynamic relationships, ΔU=q−PΔV and H=V+PV ,derive the relationship ΔH=qp.
To derive the relationship ΔH=qp starting from the thermodynamic relationships ΔU=q−PΔV and H=U+PV, we can follow these steps:
Step 1: Start with the first law of thermodynamics
We begin with the equation:
ΔU=q−PΔV
Rearranging this gives us:
q=ΔU+PΔV
Step 2: Use the definition of enthalpy
The enthalpy H is defined as:
H=U+PV
To find the change in enthalpy, we take the differential:
ΔH=ΔU+Δ(PV)
Step 3: Apply the product rule to Δ(PV)
Using the product rule for differentiation, we can express Δ(PV) as:
Δ(PV)=PΔV+VΔP
Substituting this back into the equation for ΔH:
ΔH=ΔU+PΔV+VΔP
Step 4: Consider constant pressure conditions
If the process occurs at constant pressure (ΔP=0), the term VΔP becomes zero:
ΔH=ΔU+PΔV
Step 5: Substitute for ΔU
Now, we can substitute our expression for q from Step 1 into the equation:
ΔH=q+0(since ΔP=0)
Thus, we have:
ΔH=qp
Final Result
We have derived the relationship:
ΔH=qp
We begin with the equation:
ΔU=q−PΔV
Rearranging this gives us:
q=ΔU+PΔV
The enthalpy H is defined as:
H=U+PV
To find the change in enthalpy, we take the differential:
ΔH=ΔU+Δ(PV)
Using the product rule for differentiation, we can express Δ(PV) as:
Δ(PV)=PΔV+VΔP
Substituting this back into the equation for ΔH:
ΔH=ΔU+PΔV+VΔP
If the process occurs at constant pressure (ΔP=0), the term VΔP becomes zero:
ΔH=ΔU+PΔV
Now, we can substitute our expression for q from Step 1 into the equation:
ΔH=q+0(since ΔP=0)
Thus, we have:
ΔH=qp
We have derived the relationship:
ΔH=qp
Topper's Solved these Questions
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - COMPETITION FOCUS (JEE ( main andAdvanced ) /Medical Entrance Special)
131 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Comprehension 1
1 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - ADDITIONAL QUESTIONS(VERY SHORT ANSWER QUESTIONS)
43 Videos
- STRUCTURE OF ATOMBOOK - PRADEEPCHAPTER - STRUCTURE OF ATOMEXERCISE - Competition Focus (JEE (Main and Advanced)/Medical Entrance (IX. Assertion And Reason Type Questions (Type II))
12 Videos
Similar Questions
Knowledge Check
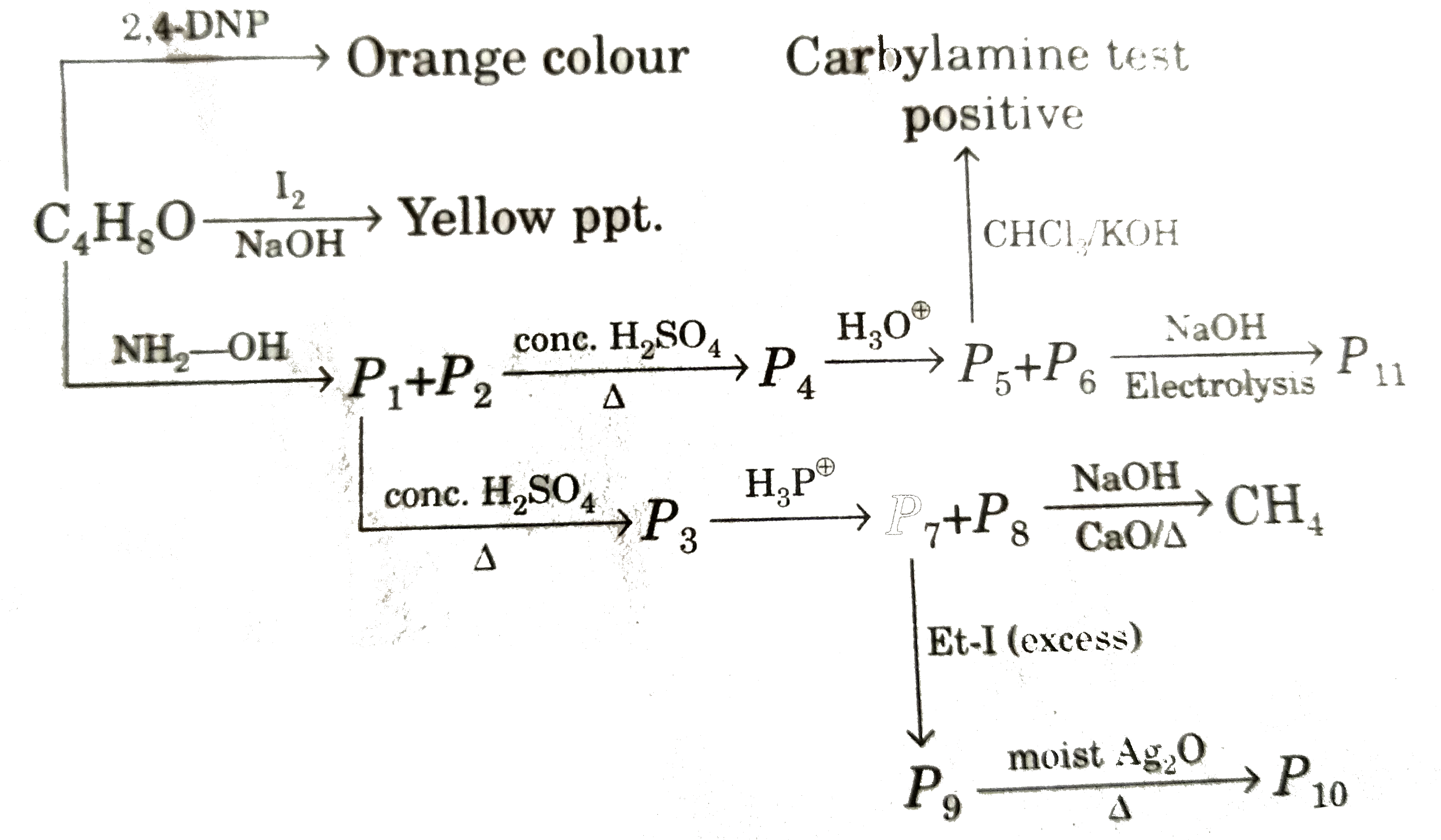
What is the relationship between P1 and P2AGeometrical isomersBOptical isormersCPositional isomersDChain isomers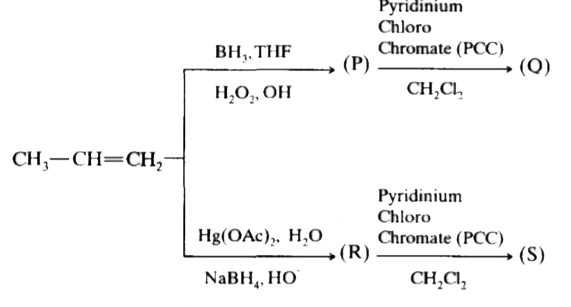
Relationship between products (Q) and (S) isApositional isomerBchain isomer.Cstereoisomer.Dfunctional isomer.The relationship between PC,VC and TC is
APCVC=RTBPCVC=3RTCCPCVC=35RTCDPCVC=38RTC
Compare the formula Cp−Cv=R for an ideal gas with the thermodynamics relation ΔU=ΔQ−PΔV.
View SolutionDerive the relationship between ΔH and ΔU for an ideal gas. Explain each term involved in the equation.
View SolutionThe relationship between PC,VC and TC is
View SolutionThe relationship between Pc,VcandTc is
View Solution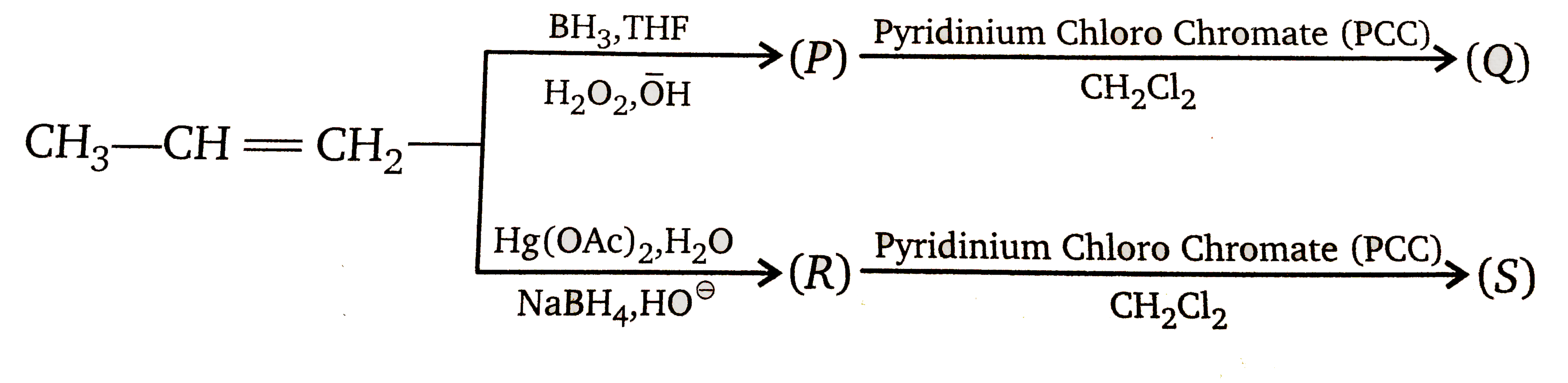
Relationship between products (Q) and (S) is :
View Solution
