Question

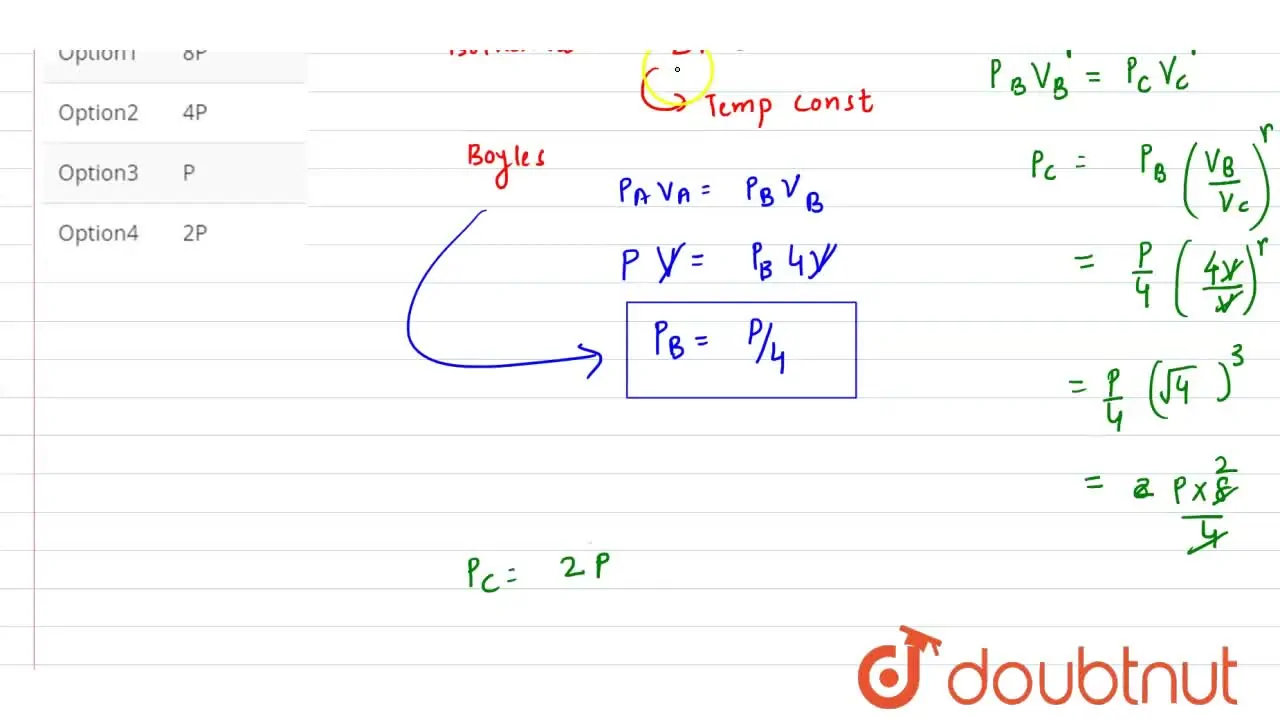
Initial pressure and volume of a gas are P and V respectively. First its volume is expanded to 4V by isothermal process and then again its volume makes to be V by adiabatic process then its final pressure is $(\gamma =1.5)$ -

Options

A. 8P
B. 4P
C. P
D. 2P

Answer

D

Explanation

To solve the problem step by step, we will analyze the two processes: the isothermal expansion and the adiabatic compression.

Step 1: Isothermal Expansion
In the first step, the gas undergoes an isothermal expansion from volume \( V \) to \( 4V \). For an isothermal process, we can use Boyle's Law, which states that the pressure of a gas is inversely proportional to its volume when the temperature is constant.

Using Boyle's Law:
\( P_1 V_1 = P_2 V_2 \)
Where:
- \( P_1 = P \) (initial pressure)
- \( V_1 = V \) (initial volume)
- \( P_2 \) is the pressure after expansion
- \( V_2 = 4V \) (final volume)

Substituting the values:
\( P \cdot V = P_2 \cdot 4V \)

Dividing both sides by \( 4V \):
\( P_2 = \frac{P}{4} \)

Step 2: Adiabatic Compression
Next, the gas undergoes an adiabatic process where its volume changes from \( 4V \) back to \( V \). For an adiabatic process, we use the relation:
\( P_1 V_1^\gamma = P_2 V_2^\gamma \)
Where:
- \( P_1 = P_2 = \frac{P}{4} \) (pressure after isothermal expansion)
- \( V_1 = 4V \) (initial volume for adiabatic process)
- \( V_2 = V \) (final volume for adiabatic process)
- \( \gamma = 1.5 \)

Substituting the values into the adiabatic equation:
\( \left(\frac{P}{4}\right) (4V)^{1.5} = P_3 V^{1.5} \)

Calculating \( (4V)^{1.5} \):
\( (4V)^{1.5} = 4^{1.5} V^{1.5} = 8 V^{1.5} \)

Now substituting this back into the equation:
\( \left(\frac{P}{4}\right) \cdot 8 V^{1.5} = P_3 V^{1.5} \)

Dividing both sides by \( V^{1.5} \):
\( \frac{P \cdot 8}{4} = P_3 \)

Simplifying:
\( P_3 = 2P \)

Final Result
The final pressure \( P_3 \) after both processes is:
\( P_3 = 2P \)