The initial volume and pressure of a gas are V and P respectively. It is expand by two different processes such that in each process the final volume becomes 2V. If the work done in isothermal change is W1 and the amount of work done in adiabatic change isW2, then
W1>W2
W1<W2
W1=W2
nothing can be said
The correct Answer is:A
To solve the problem regarding the work done in isothermal and adiabatic processes, we can follow these steps:
Step 1: Understand the Initial Conditions
The initial volume (V) and pressure (P) of the gas are given. The gas expands to a final volume of 2V in both processes.
Step 2: Work Done in Isothermal Process
For an isothermal process, the work done W1 can be calculated using the formula:
W1=P⋅V⋅ln(VfVi)
Here, Vf=2V and Vi=V. Thus, we can substitute these values:
W1=P⋅V⋅ln(2VV)=P⋅V⋅ln(2)
Step 3: Work Done in Adiabatic Process
For an adiabatic process, the work done W2 can be calculated using the formula:
W2=1γ−1(P1V1−P2V2)
Where P1 and V1 are the initial pressure and volume, and P2 and V2 are the final pressure and volume.
Using the adiabatic condition PVγ=constant, we can express P2 as:
P2=P1(V1V2)γ=P(V2V)γ=P(12)γ=P2γ
Now substituting P2 into the work done formula:
W2=1γ−1(PV−P2γ⋅2V)
=1γ−1(PV−P⋅2V2γ)
=PVγ−1(1−22γ)
Step 4: Compare W1 and W2
From the expressions derived, we can see:
W1=PVln(2)
W2=PVγ−1(1−22γ)
To compare W1 and W2, we need to analyze the factors involved. Since the logarithmic function grows slower than polynomial functions, and given that γ>1, it can be inferred that:
W1>W2
Conclusion
Thus, we conclude that the work done in the isothermal process W1 is greater than the work done in the adiabatic process W2:
W1>W2
The initial volume (V) and pressure (P) of the gas are given. The gas expands to a final volume of 2V in both processes.
For an isothermal process, the work done W1 can be calculated using the formula:
W1=P⋅V⋅ln(VfVi)
Here, Vf=2V and Vi=V. Thus, we can substitute these values:
W1=P⋅V⋅ln(2VV)=P⋅V⋅ln(2)
For an adiabatic process, the work done W2 can be calculated using the formula:
W2=1γ−1(P1V1−P2V2)
Where P1 and V1 are the initial pressure and volume, and P2 and V2 are the final pressure and volume.
P2=P1(V1V2)γ=P(V2V)γ=P(12)γ=P2γ
W2=1γ−1(PV−P2γ⋅2V)
=1γ−1(PV−P⋅2V2γ)
=PVγ−1(1−22γ)
From the expressions derived, we can see:
W1=PVln(2)
W2=PVγ−1(1−22γ)
W1>W2
Thus, we conclude that the work done in the isothermal process W1 is greater than the work done in the adiabatic process W2:
W1>W2
Topper's Solved these Questions
- ThermodynamicsBook:MOTIONChapter:ThermodynamicsExercise:EXERCISE - 2
Explore 40 Videos
- ThermodynamicsBook:MOTIONChapter:ThermodynamicsExercise:EXERCISE - 3 SECTION - A
Explore 49 Videos
- ThermodynamicsBook:MOTIONChapter:ThermodynamicsExercise:Solved Example
Explore 10 Videos
- SURFACE TENSION & VISCOSITY Book:MOTIONChapter:SURFACE TENSION & VISCOSITY Exercise:Exercise - 4 | Level-II Previous Year | JEE Advanced
Explore 12 Videos
- UNIT & DIMENSIONSBook:MOTIONChapter:UNIT & DIMENSIONSExercise:Exercise - 4 (Level - II) (PREVIOUS YEAR JEE ADVANCED)
Explore 10 Videos
Similar Questions
A gas is expanded to double its volume by two different processes. One is isobaric and the other is isothermal. Let W1 and W2 be the respective work done, then find W1 and W2
View SolutionThe figures given below show different processes (relating pressure P and volume V) for a given amount of an ideal gas. W is work done by the gas and ΔQ is heat absorbed by the gas.
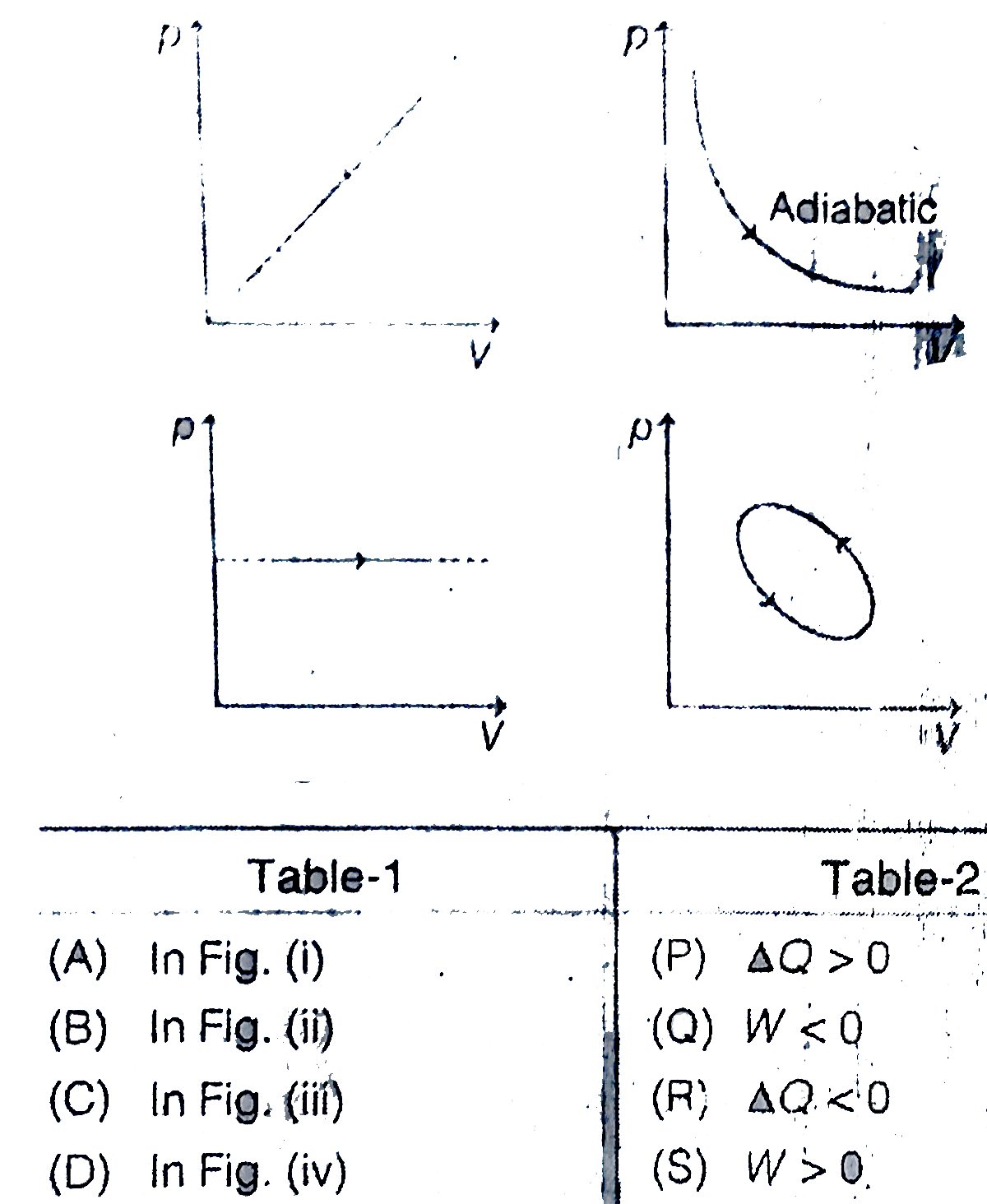
View Solution
Knowledge Check
The pressure and volume of a gas are P and V. If its pressure is reduced to P/2, by (A) isothermal process (B) by adiabatic process then the final volume will be :
Amore in ABmore in BCequal in A and BDdepends on the nature of gasInitial pressure and volume of a gas are P and V respectively. First its volume is expanded to 4V by isothermal process and then again its volume makes to be V by adiabatic process then its final pressure is (γ=1.5) -
A8PB4PCPD2PTwo moles of a gas is expanded to double its volwne by two different processes. One is isobaric and the other is isothermal. If W1 and W2are the works done respectively, then
Aw2=W1ln2BW2=W1CW2=W1ln2DW21=W2ln2
Consider one mole of helium gas enclosed in a container at initial pressure P1and volume V1 . It expands isothermally to volume V1 After this , the gas expands adiabatically and its volume becomes 32V1 . The work done by the gas during isothermal and adiabatic expansion processes are WisoandWadia respectively . if the radio WisoWadia=fIn2, then f is __________ .
View SolutionInitial pressure and volume of a gas are P and V respectively. First it is expanded isothermally to volume 4 V and then compressed adiabatically to volume V. The final pressure of gas will be (given γ=32)
View SolutionA gas expands under constant pressure P from volume V1 toV2The work done by the gas is
View SolutionAn ideal gas has initial volume V and pressure p. In doubling its volume the minimum work done will be in the process (of the given processes)
View SolutionAn ideal gas at pressure P and volume V is expanded to volume 2V. Column I represents the thermodynamic process used during expansion. Column II represents the work done during processes in the random order.

View Solution

