Concentric circles of radii 1,2,3,....,100cm are drawn. The interior of the smallest circle is colored red and the angular regions are colored alternately green and red, so that no two adjacent regions are of the same color. Then, the total area of the green regions in sq. cm is equal to 1000π b. 5050π c. 4950π d. 5151π
1000 π
5050 π
4950 π
5151 π
The correct Answer is:B

Area of green regions
=π[r22−r21)+(r24−r23)+…+(r2100−r299)]
=π[r1+r2+r3+r4+….+r100](∵r2−r1=r4−r3=..=r100−r99=1)
=π[1+2+3+...+100]
=5050πsq.cm
Topper's Solved these Questions
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - EXERCIESE ( MULTIPLE CORRECT ANSWER TYPE )
1 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - Exercise (Multiple & Comprehension)
65 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - Exercise 5.9
9 Videos
- PROBABILITY IIBOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - NUMARICAL VALUE TYPE
2 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - JEE Advanced Previous Year
11 Videos
Similar Questions
Concentric circles of radii 1,2,3,....,100cm are drawn. The interior of the smallest circle is colored red and the angular regions are colored alternately green and red, so that no two adjacent regions are of the same color. Then, the total area of the green regions in sq. cm is equal to 1000π b. 5050π c. 4950π d. 5151π
View SolutionConcentric circle of radii 1,2,3,.....,100 cms are drawn. The interior of smallest circle is colored red and the angular regions are colored alternately green and red , so that no two adjacent regions are of same color. The total area of green regions in sq. cm. is equals to :
View Solution
Knowledge Check
Two concentric circles with radii p cm and (p+ 2) cm are drawn on a paper. The difference between their areas is 44 sq. cm What is the value of p? (Take π=227)
A1.5B5C6D2.5
In Figure, there are shown sectors of two concentric circles of radii 7cm and 3.5cm. Find the area of the shaded region. (Use π=227).
View SolutionIn the figure, O is the centre of the circle.
m(arc PQR)=60∘
OP = 10 cm.
Find the area of the shaded region. (π=3.14,√3=1.73)

View SolutionIn the given figure, an equilateral triangle has been inscribed in a circle of radius 4 cm. Find the area of the shaded region. [Take π=3.14 and √3=1.73]

View SolutionIn the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region. [Use √3=1.73 and π=3.14]
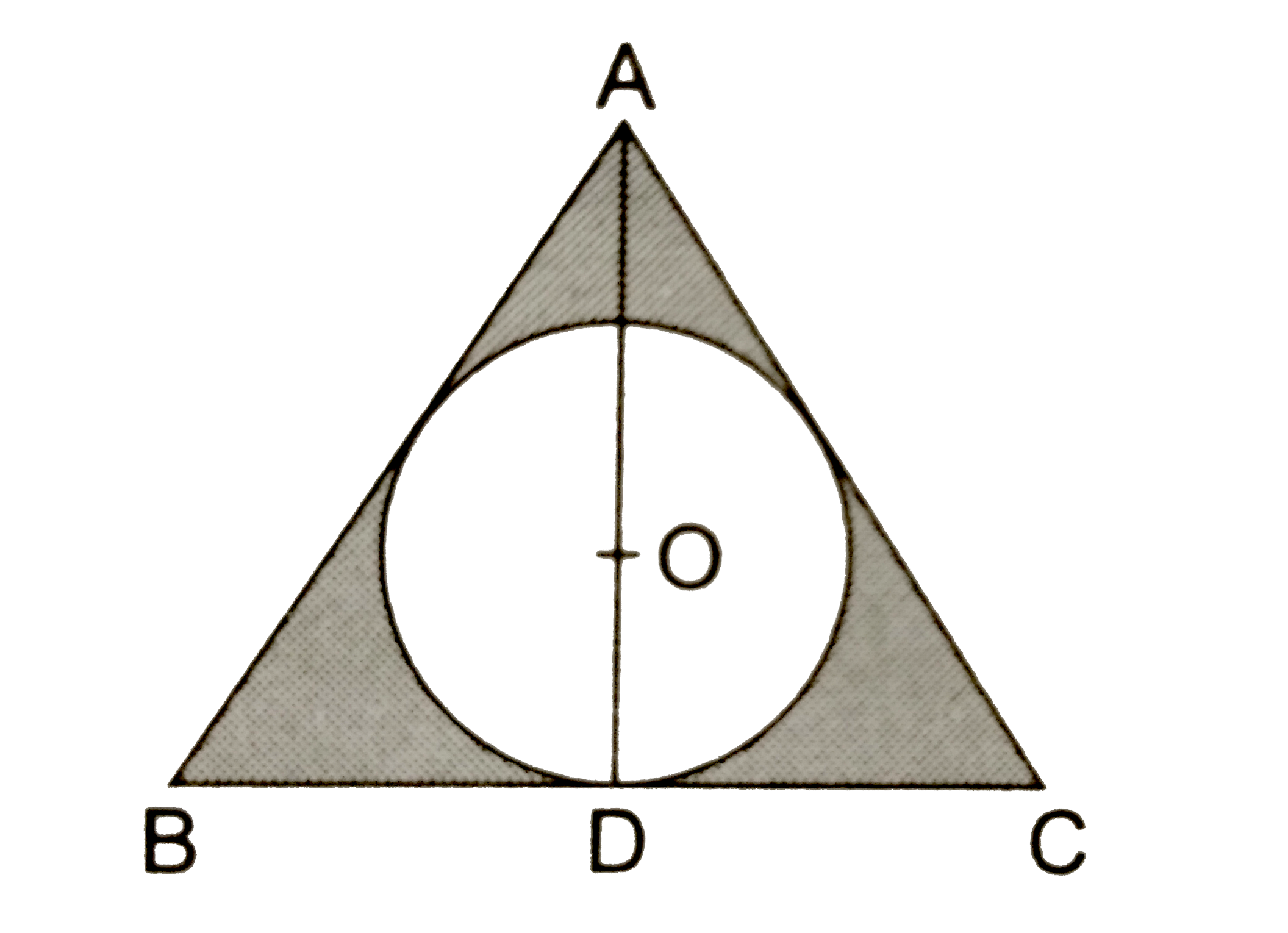
View SolutionIn the given figure ABCD is a square of side 4cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region.
[Use π=3.14]

View SolutionPQRS is a diameter of a circle of radius 6cm. The lengths PQ,QR and RS are equal. Semicircles are drawn with PQ and QS is diameters, as shown in the given figure. If PS=12cm, find the perimeter and area of the shaded region.

[Take π=3.14]
View SolutionA circle is inscribed in a square of side 14 m. The ratio of the area of the circle and that of the square is (a)π:3 (b) π:4 (c)π:2 (d) π:1
View Solution
