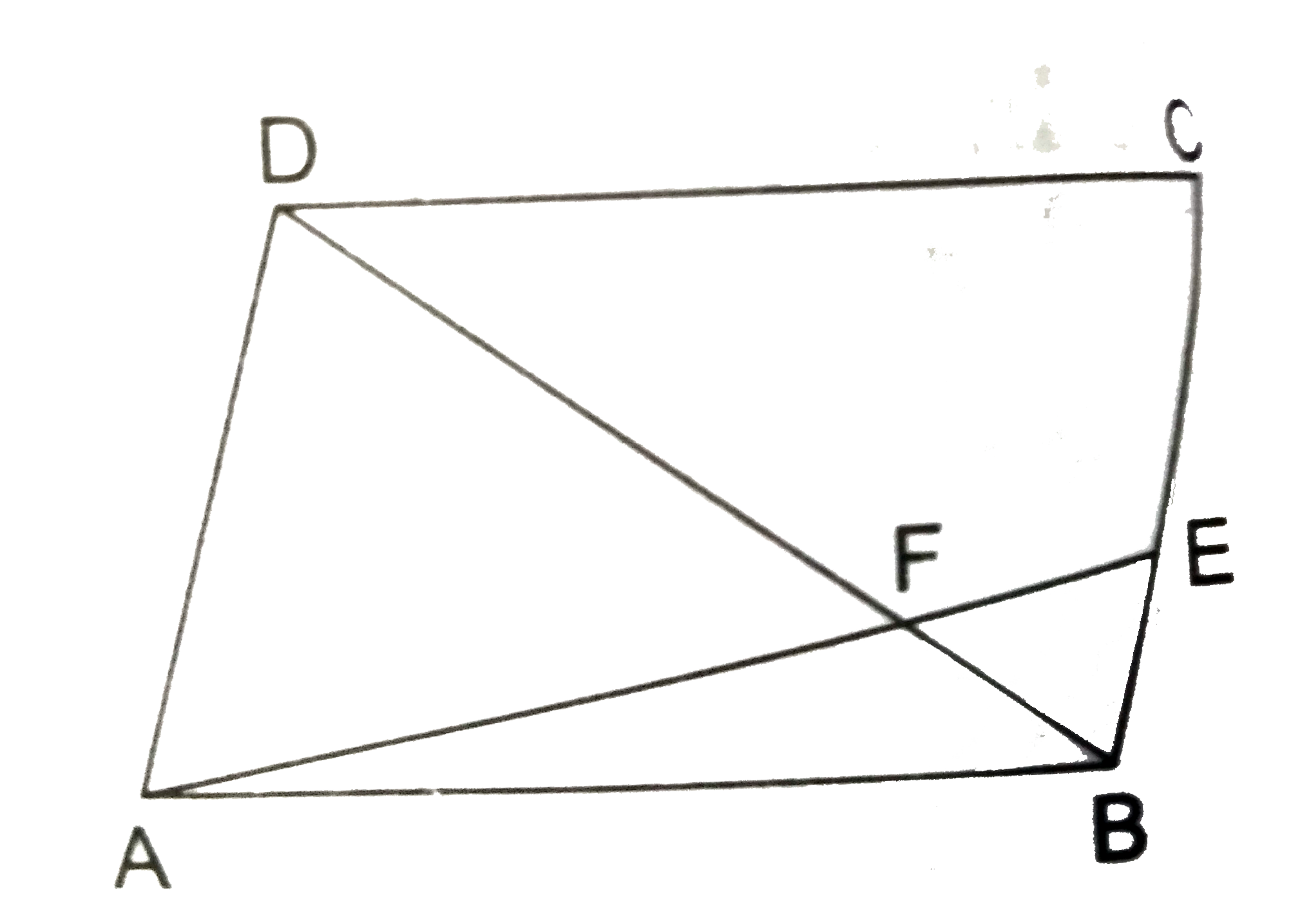
ABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point Q divides DB in the ratio
1:2
1:3
3:1
2:1
The correct Answer is:B

−−→BL=13→b
∴−−→AL=→a+13→b
Let −−→AP=λve(AL)andP divides DB in the ratio μ:1−μ. Then
−−→AP=λ→a+λ3→b (i)
Also −−→AP=μ→a+(1−μ)→b) (ii)
From (i) and (ii), λ→a+λ3→b=μ→a+(1−μ)→b
∴ λ=μandλ3=1−μ
∴ λ=34
Hence, P divides AL in the ratio 3:1 and P divides DB in the ratio 3:1.
Similarly, Q divides DB in the ratio 1:3.
Thus, DQ=14DBandPB=14DB
∴ PQ=12DB, i.e., PQ:DB=1:2
Topper's Solved these Questions
- INTRODUCTION TO VECTORS BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - MATRIX-MATCH TYPE
3 Videos
- INTRODUCTION TO VECTORS BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - Exercise (Numerical)
6 Videos
- INTRODUCTION TO VECTORS BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - LINKED COMPREHENSION TYPE
2 Videos
- INTEGRALSBOOK - CENGAGECHAPTER - INTEGRALSEXERCISE - Solved Examples And Exercises
324 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Question Bank
24 Videos
Similar Questions
Knowledge Check
ABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point P divides AL in the ratioA1:2B1:3C3:1D2:1ABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
PQ:DB is equal toA2/3B1/3C1/2D3/4In a parallelogram ABCD, a side AB is extended to E such that BE = AB. If DE cut the line BC at Q then point Q divide BC in what ratio?
A1:2B1:1C2:3D2:1
ABCD is a parallelogram. E is a point on BC such that BE : EC = m:n. If AE and DB intersect in F, then what is the ratio of the area of triangle FEB to the area of triangle AFD?
View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM. prove that LM and BD bisect each other.
View SolutionABCD is a parallelogram. P and R are the midpoints of DC and BC respectively. The line PR intersects the diagonal AC at Q . The distance CQ will be equal to
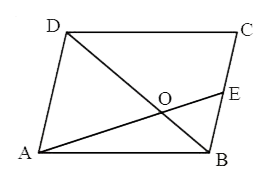
View SolutionIn the given figure, ABCD is a parallelogram. AE divides the line segment BD in the ratio 1 : 2. If BE = 1.5 cm find BC.
View SolutionIn ΔABC, P is the mid point of BC,Q divides CA internally in the ratio 2:1 and R divides AB externally in the ratio 1:2 then
View Solution