Let ABC and AB'C be two non-congruent triangles with sides BC=B'C=5, AC=6, and ∠A is fixed. If A1 and A2 are the area of the two triangles ABC and AB'C, then the value of A21+A22−2A1A2cos2A(A1+A2)2 is
9/36
25/36
25/16
16/25
The correct Answer is:B

We have cos A=62+c2−522.6.c
⇒c2−(12cosA)c+11=0
⇒c1+c2=12cosA,c1c2=11
⇒A1=12bc1sinA,A2=12bc2sinA
Given expression =(A1+A2)2−2A1.A2(2cos2A)(A1+A2)2
=1−4cos2A(A1A2(A1+A2)2)
=1−4cos2A⎛⎝14b2sin2Ac1c212b2sin2A(c1+c2)2⎞⎠
=1−4cos2A(11144×cos2A)=2536
Topper's Solved these Questions
- SOLUTIONS AND PROPERTIES OF TRIANGLE Book:CENGAGEChapter:SOLUTIONS AND PROPERTIES OF TRIANGLE Exercise:Multiple Correct Answers Type
Explore 13 Videos
- SOLUTIONS AND PROPERTIES OF TRIANGLE Book:CENGAGEChapter:SOLUTIONS AND PROPERTIES OF TRIANGLE Exercise:Comprehension Type
Explore 6 Videos
- SETS AND RELATIONSBook:CENGAGEChapter:SETS AND RELATIONSExercise:Question Bank
Explore 15 Videos
- STATISTICSBook:CENGAGEChapter:STATISTICSExercise:JEE Previous Year
Explore 10 Videos
Similar Questions
Knowledge Check
A1 and A2 are two vectors such that |A1|=3,|A2|=5 and |A1+A2|=5 the value of (2A1+3A2).(2A1−2A2) is
A2372B−123C−3372D3372If G1,G2 are centroids of triangles A1,B1,C1 and A2,B2,C2 respectively, then ¯¯¯¯¯¯¯¯¯A1A2+¯¯¯¯¯¯¯¯¯B1B2+¯¯¯¯¯¯¯¯¯C1C2=
A¯¯¯¯¯¯¯¯¯G1G2B2¯¯¯¯¯¯¯¯¯G1G2C3¯¯¯¯¯¯¯¯¯G1G2D4¯¯¯¯¯¯¯¯¯G1G2If a1anda2 aare two non- collineaar unit vectors and if |a1+a2|=√3, ,then value of (a1−a2).(2a1−a2) is
A2B32C12D1
Let A1A2A3……………….A14 be a regular polygon with 14 sides inscribed in a circle of radius 7 cm. Then the value of (A1A3)2+(A1A7)2+(A3A7)2 (in square cm) is……………..
View SolutionIf A,A1,A2 and A3 are the areas of the inscribed and escribed circles of a triangle, prove that 1√A=1√A1+1√A2+1√A3
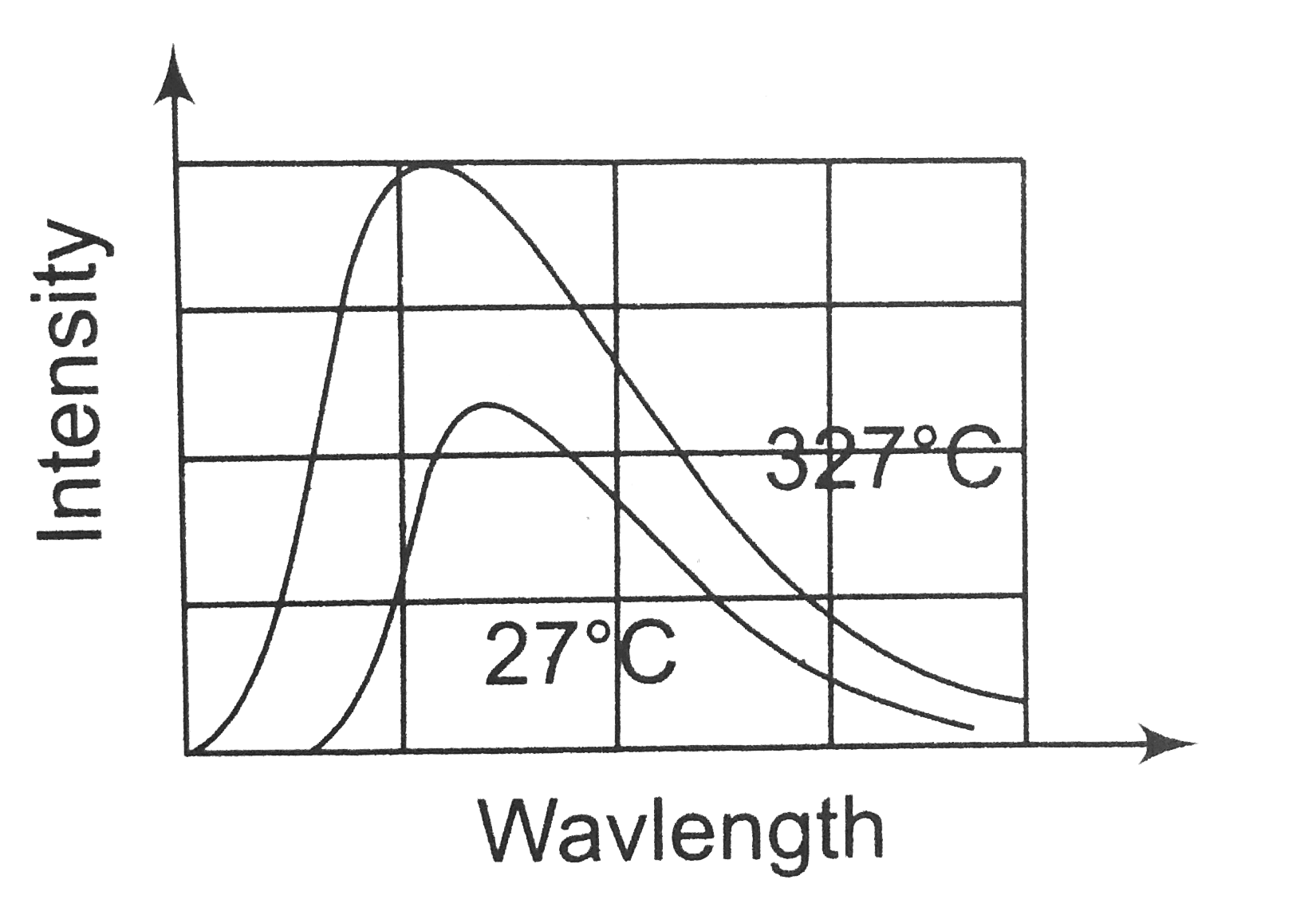
View SolutionThe spectrum of a black body at two temperatures 27∘C and 327∘C is shown in the figure. Let A1 and A2 be the areas under the two curves respectively. Find the value of A2A1
View SolutionIn triangle ABC,∠A>π2.AA1andAA2 are the medium and altitude, espectively. If ∠BAA1=∠A1AA2=∠A2AC, then sin3A3.CosA3 is equal to
View SolutionIf a1,a2,a3,a4,a5 are consecutive terms of an arithmetic progression with common difference 3, then the value of ∣∣ ∣ ∣∣a23a2a1a24a3a2a25a4a3∣∣ ∣ ∣∣ is
View Solution
