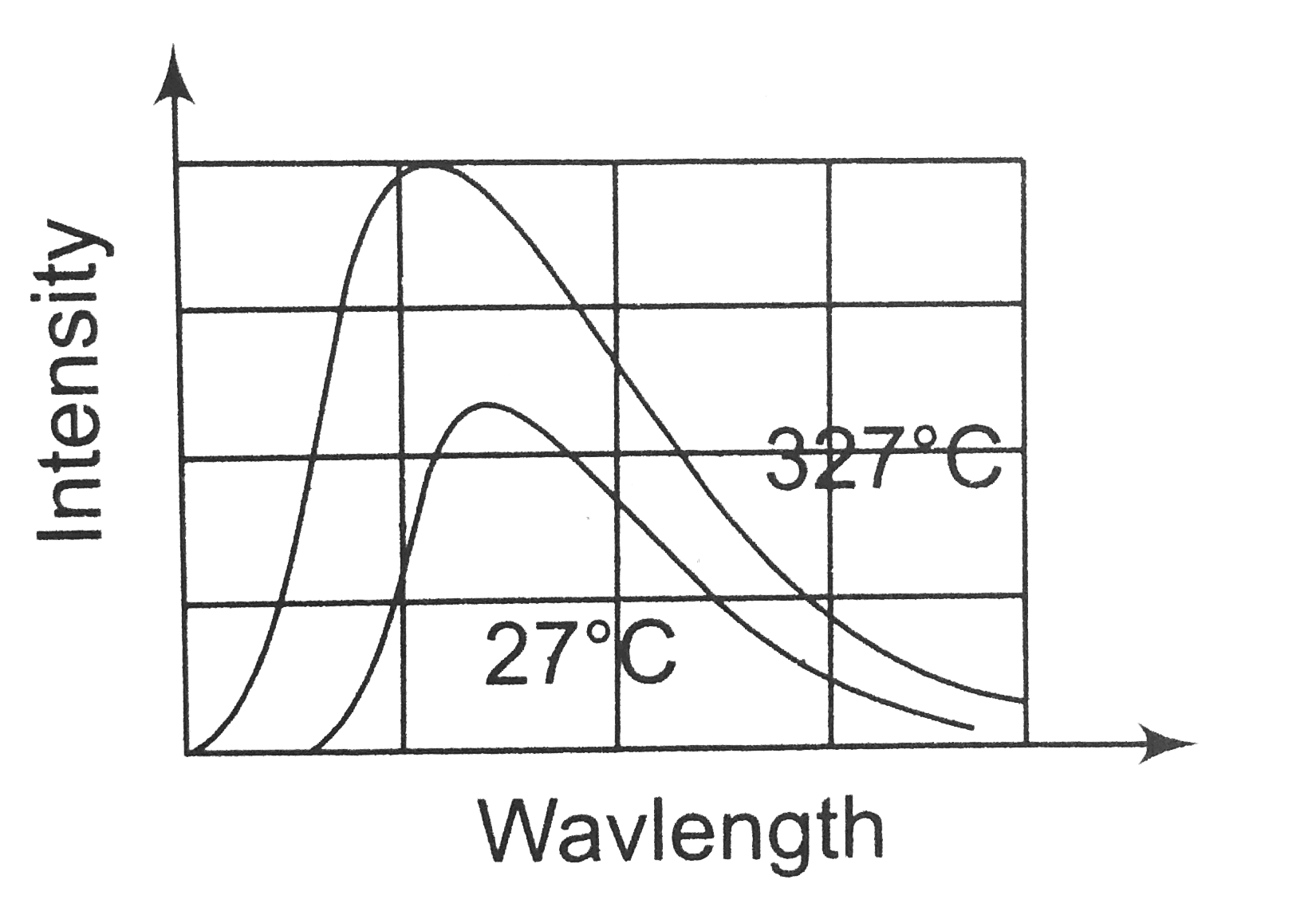
The spectrum of a black body at two temperatures 27∘C and 327∘C is shown in the figure. Let A1 and A2 be the areas under the two curves respectively. Find the value of A2A1
16:1
8:1
9:4
16:9
The correct Answer is:A
Area under given curve represents emissive power and emissive power ∝T4⇒A∝T4
⇒A2A1=T42T41=(273+327)4(273+27)4=(600300)4=161.
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Problems Baesd On Mixed Concepts
Explore 18 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Assertion Reasoning
Explore 21 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Transmission Of Heat : Conduction
Explore 28 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Chapter Test
Explore 29 Videos
- UNIT, DIMENSION AND ERROR ANALYSISBook:A2ZChapter:UNIT, DIMENSION AND ERROR ANALYSISExercise:Chapter Test
Explore 28 Videos
Similar Questions
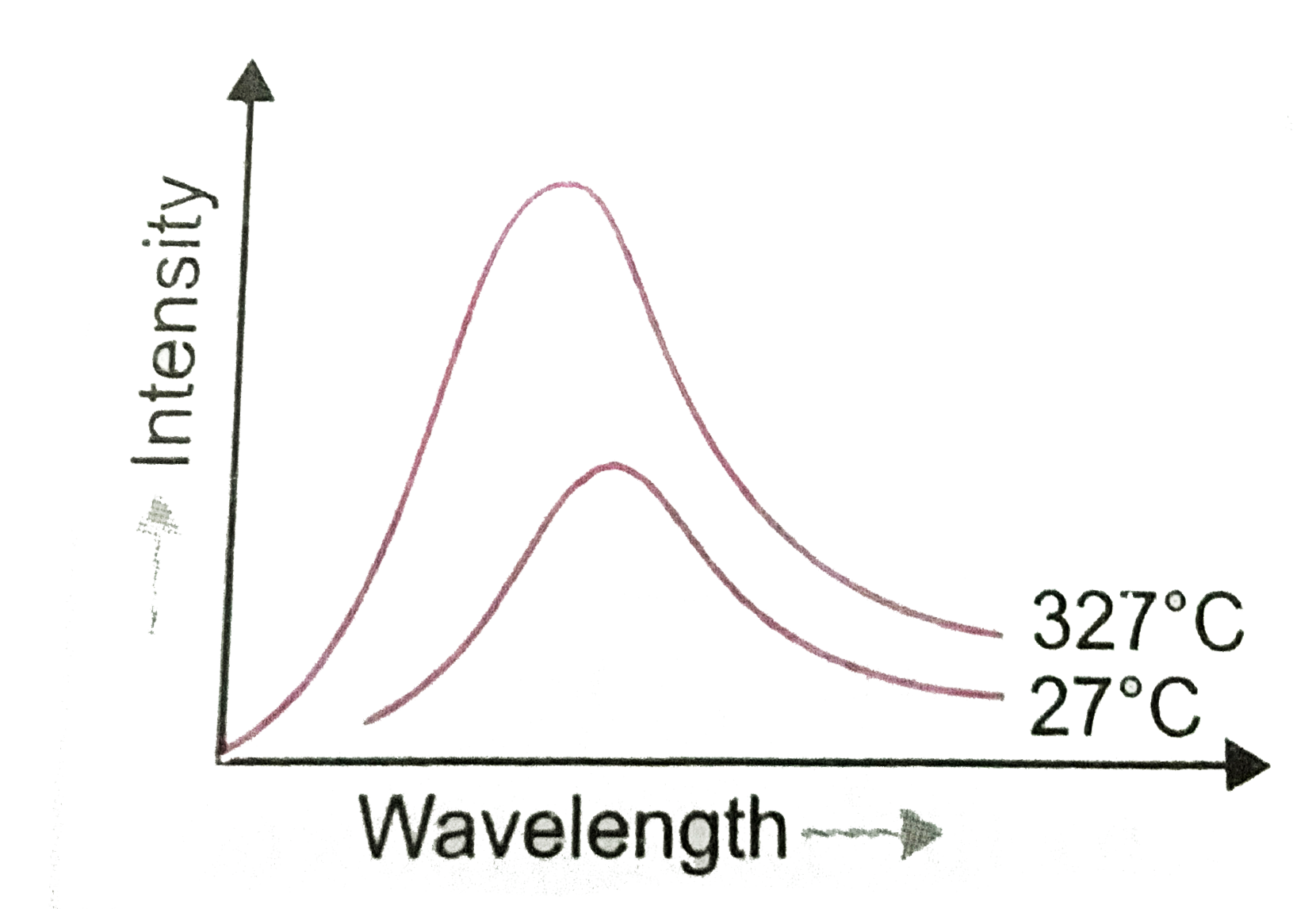
The specturm of a black body at two temperatures 27∘C and 327∘C is show in the Fig. 7(e).20. Let A1 and A2 be the respective areas tunder the two curved. Estimate the ratio A2/A1.
View SolutionIf a1,a2,a3 are the last three digits of 17256 respectively then the value of a2−a1−a3 is equal
View Solution
Knowledge Check
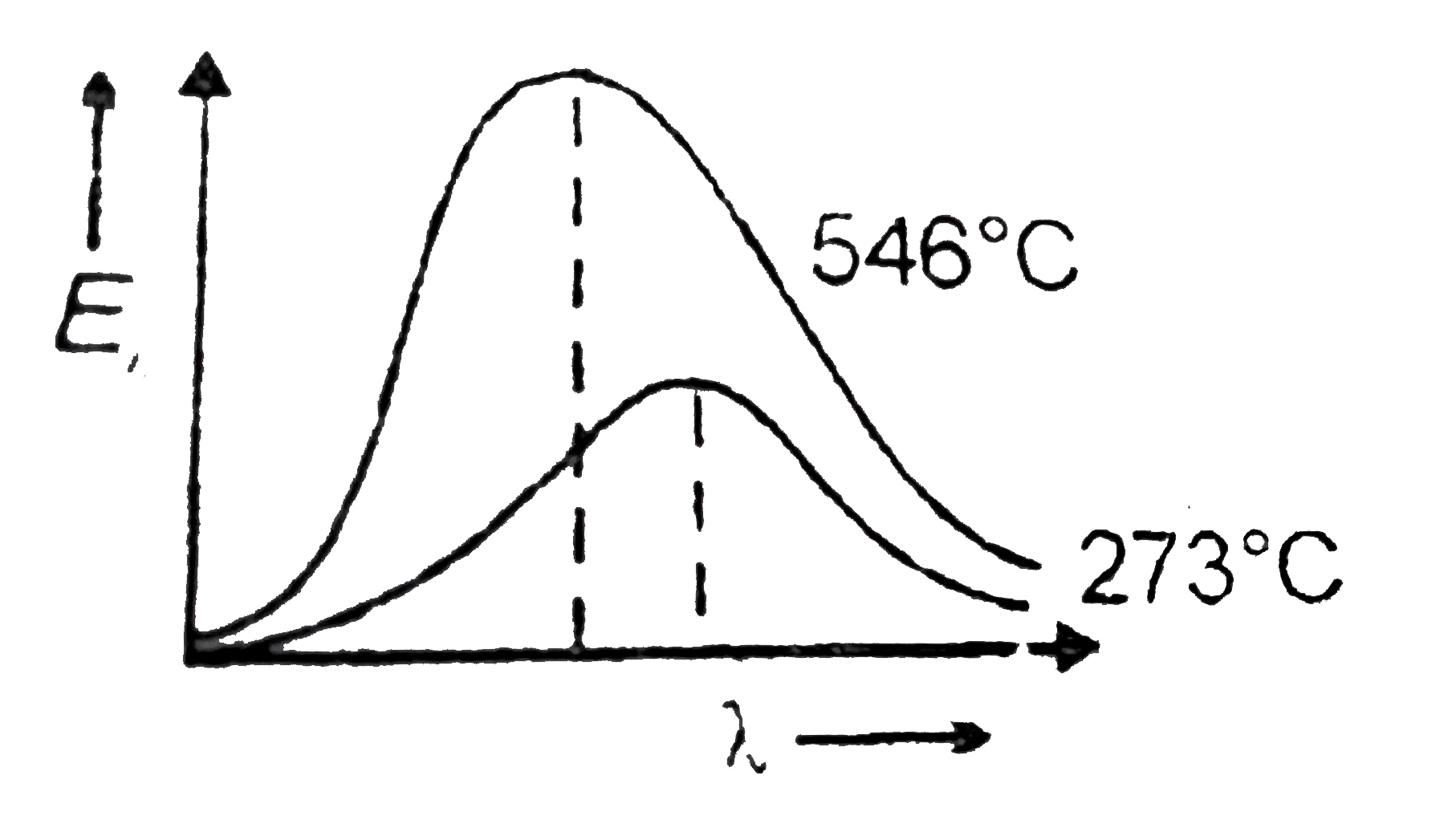
The spectra of a black body at temperatures 273∘C and 546∘C are shown in the figure. If A1 and A2 be area under the two curves respectively, the value of A2A1 is
 A8116B161C278D1681
A8116B161C278D1681A regular pentagons is inscribed in a circle. If A1 and A2 represents the area of circle and that of regular pentagon respectively, then A1:A2 is
Aπ5cos(2π)5B2π5sin(2π)5C2π5 cosec 2π5D2π5cos(2π)5Let ABC and AB'C be two non-congruent triangles with sides BC=B'C=5, AC=6, and ∠A is fixed. If A1 and A2 are the area of the two triangles ABC and AB'C, then the value of A21+A22−2A1A2cos2A(A1+A2)2 is
A9/36B25/36C25/16D16/25
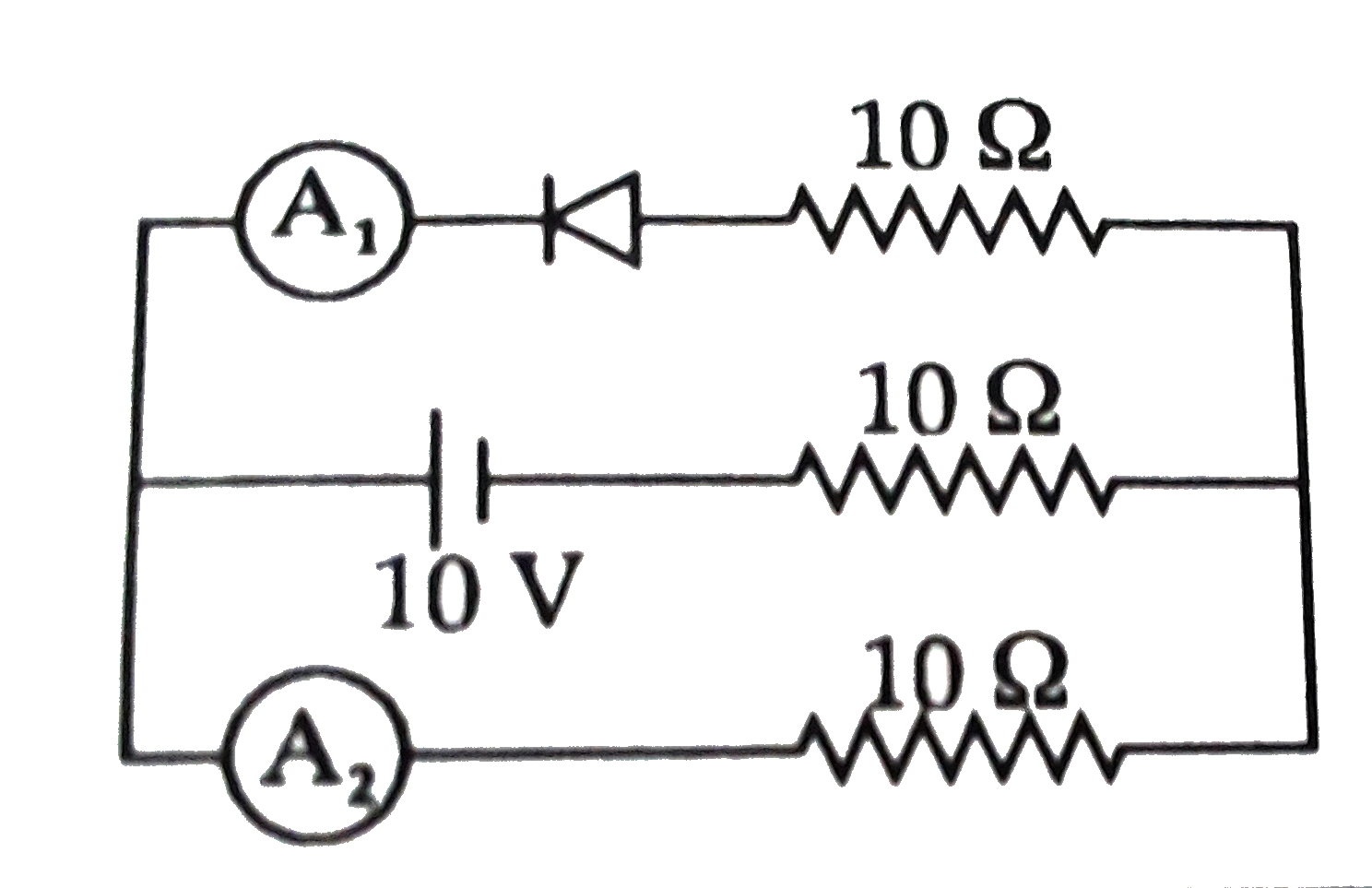
In the figure shown the readings of the ammeters A1andA2 are respectively.
View SolutionIf the area of the circle is A1 and the area of the regular pentagon inscribed in the circle is A2, then find the ratio A1A2.
View SolutionLet a and b be two positive real numbers such that a+2b≤1. Let A1 and A2 be, respectively, the areas of circles with radii ab3 and b2. Then the maximum possible value of A1A2 is:
View SolutionIf A1 and A2 be areas of two regular polygons having the same perimeter and number of sides be n and 2n respectively, then : A1A2 is
View SolutionIf a1anda2 aare two non- collineaar unit vectors and if |a1+a2|=√3, ,then value of (a1−a2).(2a1−a2) is
View Solution

