Equivalent resistance between the adjacent corners of a regular n–sided polygon of uniform wire of resistance would be :
The correct Answer is:D
To find the equivalent resistance between the adjacent corners of a regular n-sided polygon made of a uniform wire of resistance R, we can follow these steps:
1. Understanding the Problem:
We have a regular n-sided polygon, and we need to find the equivalent resistance between two adjacent corners (let's call them A and B). The total resistance of the wire forming the polygon is R.
2. Resistance of Each Edge:
Since the polygon has n sides, the resistance of each edge (R_edge) can be calculated as:
Redge=Rn
3. Identifying the Configuration:
When looking at the polygon, the two adjacent corners A and B are connected by two edges:
- One edge directly between A and B.
- The other edge connects A to the next corner (let's call it C) and then C to B.
4. Resistance Values:
- The resistance of the direct edge AB is Redge=Rn.
- The resistance of the path A to C to B consists of two edges, which is:
RAC+RCB=Rn+Rn=2Rn
5. Equivalent Resistance Calculation:
Now, we have two resistances in parallel:
- R1=Rn (direct edge AB)
- R2=2Rn (path ACB)
The formula for equivalent resistance Req for two resistors in parallel is:
1Req=1R1+1R2
Substituting the values:
1Req=1Rn+12Rn=nR+n2R=nR+n2R=2n+n2R=3n2R
Therefore, the equivalent resistance Req is:
Req=2R3n
6. Final Result:
The equivalent resistance between the adjacent corners of a regular n-sided polygon of uniform wire of resistance R is:
Req=2R3n
We have a regular n-sided polygon, and we need to find the equivalent resistance between two adjacent corners (let's call them A and B). The total resistance of the wire forming the polygon is R.
Since the polygon has n sides, the resistance of each edge (R_edge) can be calculated as:
Redge=Rn
When looking at the polygon, the two adjacent corners A and B are connected by two edges:
- One edge directly between A and B.
- The other edge connects A to the next corner (let's call it C) and then C to B.
- The resistance of the direct edge AB is Redge=Rn.
- The resistance of the path A to C to B consists of two edges, which is:
RAC+RCB=Rn+Rn=2Rn
Now, we have two resistances in parallel:
- R1=Rn (direct edge AB)
- R2=2Rn (path ACB)
1Req=1R1+1R2
1Req=1Rn+12Rn=nR+n2R=nR+n2R=2n+n2R=3n2R
Req=2R3n
The equivalent resistance between the adjacent corners of a regular n-sided polygon of uniform wire of resistance R is:
Req=2R3n
Topper's Solved these Questions
Similar Questions
Knowledge Check
find the equivalent resistance between A and E(resistance of each resistor is R.
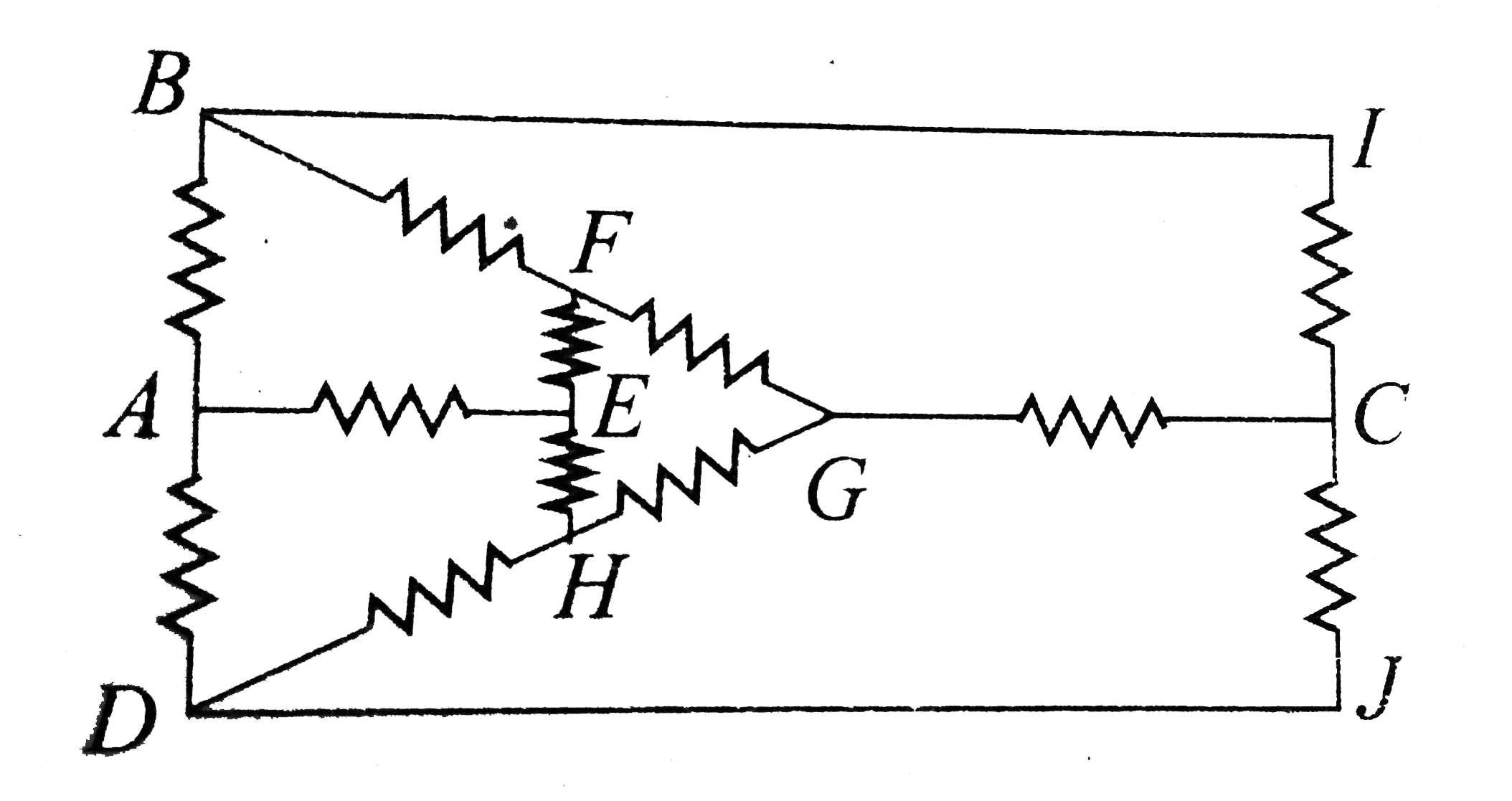 A712RB713RC715RD813R
A712RB713RC715RD813RFind equivalent resistance between point A and B in the adjacent circuit. (Each resistor has resistance R)
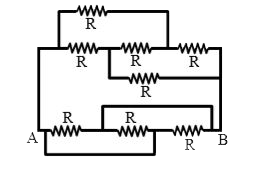 AR3BR4CRDR2
AR3BR4CRDR2A uniform wire of resistance R is slaped into a regular n-sided polygon (n is seven). The equivalent resistance between any two corners can have :
Athe maximum value R/4Bthe maximum value R/nCthe minimum value R(n−1n2)Dthe minimum value R/n
Find equivalent resistance between points A and B in the figure. Each resistance is R.

View SolutionA uniform wire of resistance R is shaped into a regular n−sided polygon (n is even), The equivalent resistance between any two corners can have.
(i) the maximum value R4
(ii) the minimum value Rn
(iii) the minimum value R(n−1n2)
(iv) the minimum value Rn.
View SolutionA uniform wire of 16Ω resistance is made into the form of a square. Two opposite corners of square are connected by a wire of resistance 16Ω. The effective resistance between the other two opposite corners is
View SolutionIf r is the radius of inscribed circle of a regular polygon of n-sides ,then r is equal to
View SolutionThe equivalent resistance between the points A and B is (R is the resistance of each side of smaller square)

View Solution

