A point particle moves along a straight line such that where t is time. Then ratio of acceleration to cube of the velocity is
The correct Answer is:B
Similar Questions
The acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
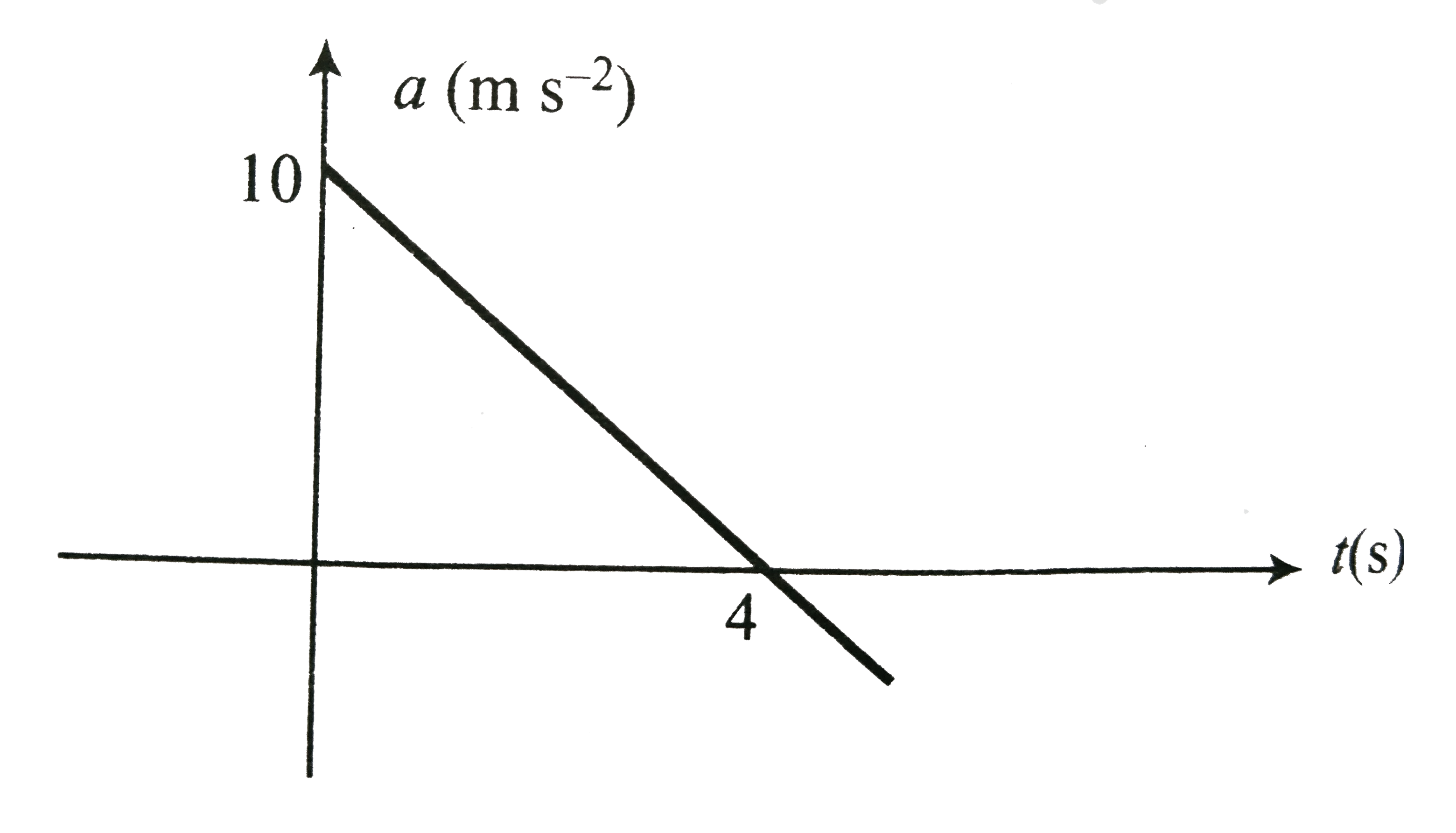 .
.
View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
 .
.
View Solution
Knowledge Check
The acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
 .A12sB5sC8sD16s
.A12sB5sC8sD16sThe acceleration-time graph of a particle moving along a straight line is as shown in figure. At what time the particle acquires its initial velocity ?
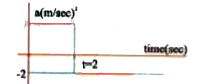 A12 sec.B6 sec.C8 sec.D16 sec.
A12 sec.B6 sec.C8 sec.D16 sec.The speed v of a particle moving along a straight line is given by a+bv2=x2 (where x is its distance from the origin). The acceleration of the particle is
AbxBx/aCx/bDx/ab
The acceleration time graph of a particle moving along a straight line is as shown in Fig.At what time the particle acquires its initial velocity?
View SolutionFigure shows the acceleration-time graph of a particle moving along a straight line. After what time the particle acquires its initial velocity?

View SolutionFigure shows the acceleration-time graph of a particle moving along a straight line. After what time the particle acquires its initial velocity?

View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View Solution
