Suppose ABCDEF is a hexagon such that AB=BC=CD=1 and DE=EF=FA=2. If the vertices A,B,C,D,E,F, are concylic, the radius of the circle passing throught them is-
√52
√73
√113
√2
The correct Answer is:B
Step by step video & text solution for Suppose ABCDEF is a hexagon such that AB=BC=CD=1 and DE=EF=FA=2. If the vertices A,B,C,D,E,F, are concylic, the radius of the circle passing throught them is- by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
If AB =112cm, BC=16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is
A90∘B120∘C60∘D150∘ - Question 2 - Select One
If ABCDEF is a regular hexagon , then A→D+E→B+F→C equals
A2A→BB→0C3A→BD4A→B - Question 3 - Select One
Let A, B, C, D be points on a vertical line such that AB = BC = CD. If a body is released from position A, the times of descent through AB, BC and CD are in the ratio.
A1:(√3−√2):(√3+√2)B1:(√2−1):(√3−√2)C1:(√2−1):√3D1:√2:(√3−1)
ABCDEF is a regular hexagon. With vertices A, B, C, D, E and F as the centres, circles of same radius ‘r’ are drawn. Find the area of the shaded portion shown in the given figure.
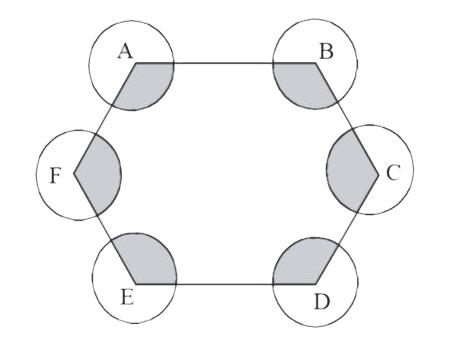 View Solution
View SolutionLet ABCDEF be a regular hexagon and −−→AB=→a,−−→BC=→b,−−→CD=→c then −−→AE is
View SolutionLet ABCDEF be a regular hexagon whose centre is at the origin. (A,B,C,D,EandF are in anticlockwise direction). If the coordinates of A be 1+i then C lies in
View SolutionThe equiangular convex hexagon ABCDEF has AB=1,BC=4,CD=2,andDE=4. The area of the hexagon is
View SolutionAB and CD are two parallel chords of a circle such that AB = 6 cm and CD = 2AB. Both chords are on the same side of the centre of the circle. If the distance between is equal to one-fourth of the length of CD, then the radius of the circle is-
AB और CD किसी वृत्त की दो ऐसी समानांतर जीवाएं है कि AB = 6 सेमी है और CD = 2AB है | दोनों जीवाएं वृत्त के केंद्र के एक ही तरफ हैं | यदि बीच की दूरी CD की लंबाई के एक चौथाई के बराबर है, तो वृत्त की त्रिज्या ज्ञात करें |View Solution
