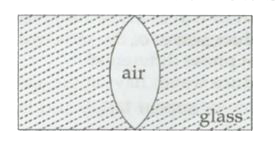
In figure, an air lens of radius of curvature of each surface equal to 10cm is cut into a cylinder of glass of refractive index 1.5. The focal length and the nature of lens are

15 cm, concave
15 cm, convex
∞, neither concave nor convex
0, concave
The correct Answer is:A
1f=(nag−1)(1R1−1R2)
⇒ 1f=(23−1)(110+110)
⇒1f=−13×210⇒f=15 cm .
Hence, behave as concave lens.
Similar Questions
A double convex lens of radius of curvature of each surface equal to 20 cm is made of glass of refractive index 1.5. Find the ratio of the powers of the lens when placed in air to its power when placed in water. Take refractive index of water = 1.33.
View SolutionThe radius curvature of each surface of a convex lens of refractive index 1.5 is 40 cm. Calculate its power.
View Solution
Knowledge Check
The radius of curvature of each surface of a biconcave lens made up of glass of refrative indx 1.5 is 30 cm. the focal length of the lens is
A60 cmB30 cmC−30cmD−60cmIn the figure, an air lens is cut a cylinder of glass of refractive index 1.5 . The nature of the lens is
 AdiverigingBconvergingCneither diverging nor convergingDnone of these
AdiverigingBconvergingCneither diverging nor convergingDnone of theseThe radius of curvature of each surface of a lens is 40 cm. Its refractive index is 1.5. The focal length of lens will be
A40 cmB20 cmC80 cmD30 cm
The radius of curvature for a convex lens is 40 cm , for each surface. Its refractive index is 1.5. The focal length will be
View SolutionAn equiconcave lens having radius of curvature of each surface 20 cm has one surface silvered. If the refractive index of the lens is 1.5, then the magnitude of the focal length is
View SolutionA diverging lens of focal length 10 cm having refractive index 1.5 is immersed in a liquid of refractive index 3. The focal length and nature of the lens in liquid is
View SolutionIf the radii of curvature of the two surfaces of a concave lens are 10 cm and 20 cm respectively and the refractive index is 1.5. What is its focal length ?
View SolutionThe radius of curvature of the convex face of a plano convex lens is 12cm and the refractive index of the material of the lends 1.5. Then, the focal length of the lens is
View Solution
