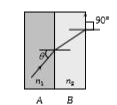
A and B are two parallel sided transparent slabs of refractive indices respectively. A ray is incident at an angle on the surface of separation of A and B and after refraction from B into air grazes the surface of B. Then
The correct Answer is:B
From Snell.s law
Similar Questions
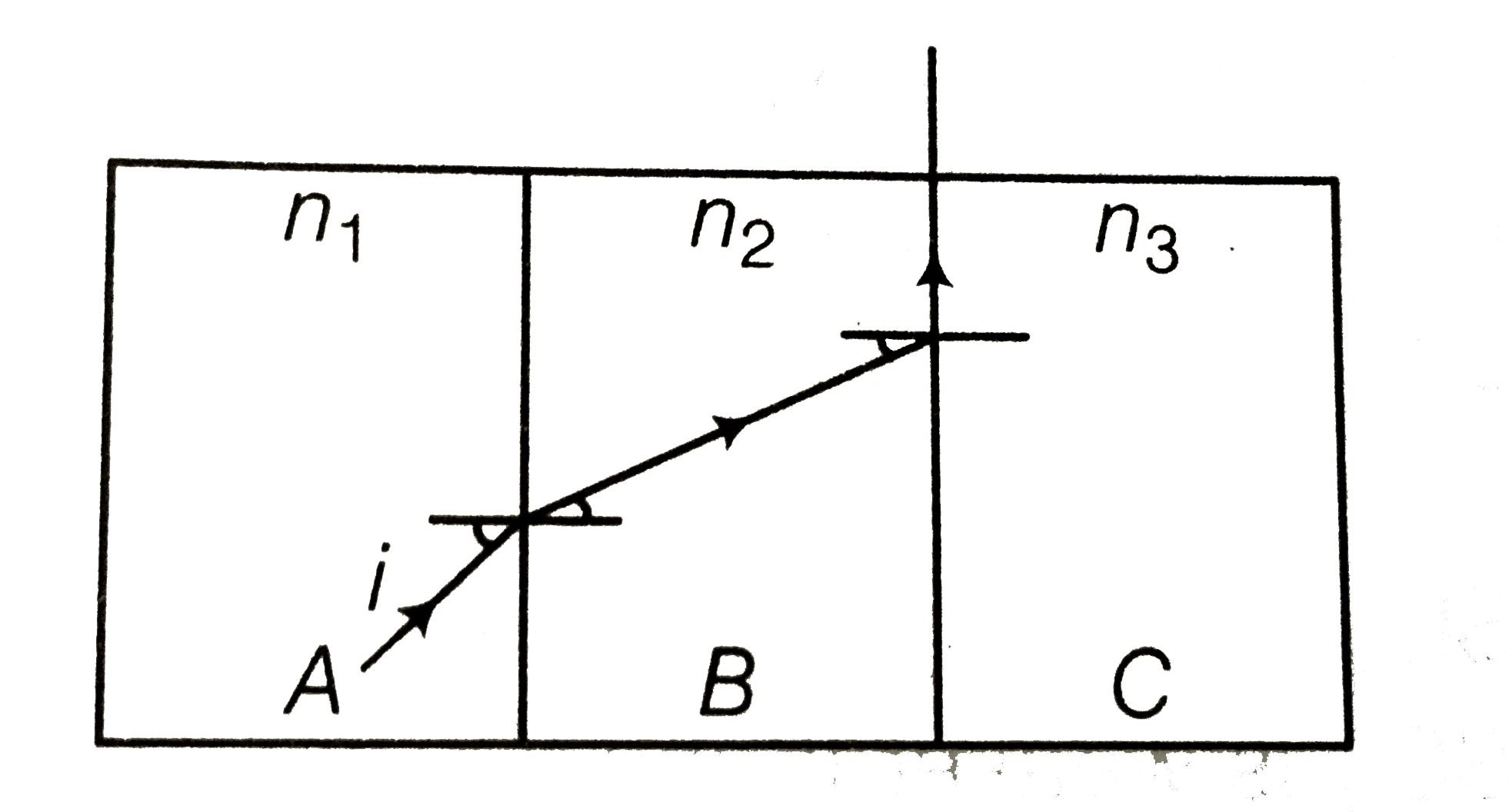
A,B, and C are the parallel sided transparent media of refractive indices n1,n2 and n3 respectively. They are arranged as shown in the figure. A ray is incident at an angle i on the surface of separation of A and B which is as shown in the figure. After the refraction into the medium B the ray grazes the surfaces of separation of the media B and C. then sini equal to
 View Solution
View SolutionA equilateral glass prism has a refractive index √(2) . A light ray is incident at 45^∘ on one face.Total deviation of ray after refraction from second surface is n times15^(0) where 'n' is
View Solution
Knowledge Check
- Question 1 - Select One
AN unpolarised beam of light is incident at the polarising angle on the surface of a transparent medium of refractive index 1.6. The angle of refraction in the medium is
A58∘B29∘C32∘D42∘ - Question 2 - Select One
A rectangular glass slab ABCD of refractive index n1 is immersed in water of refractive index n2(n1<n2). A ray of light is incident at the surface AB of the slab as shwon. The maximum value of the angle of incidence αmax such that the ray comes out from the other surface CD is given by
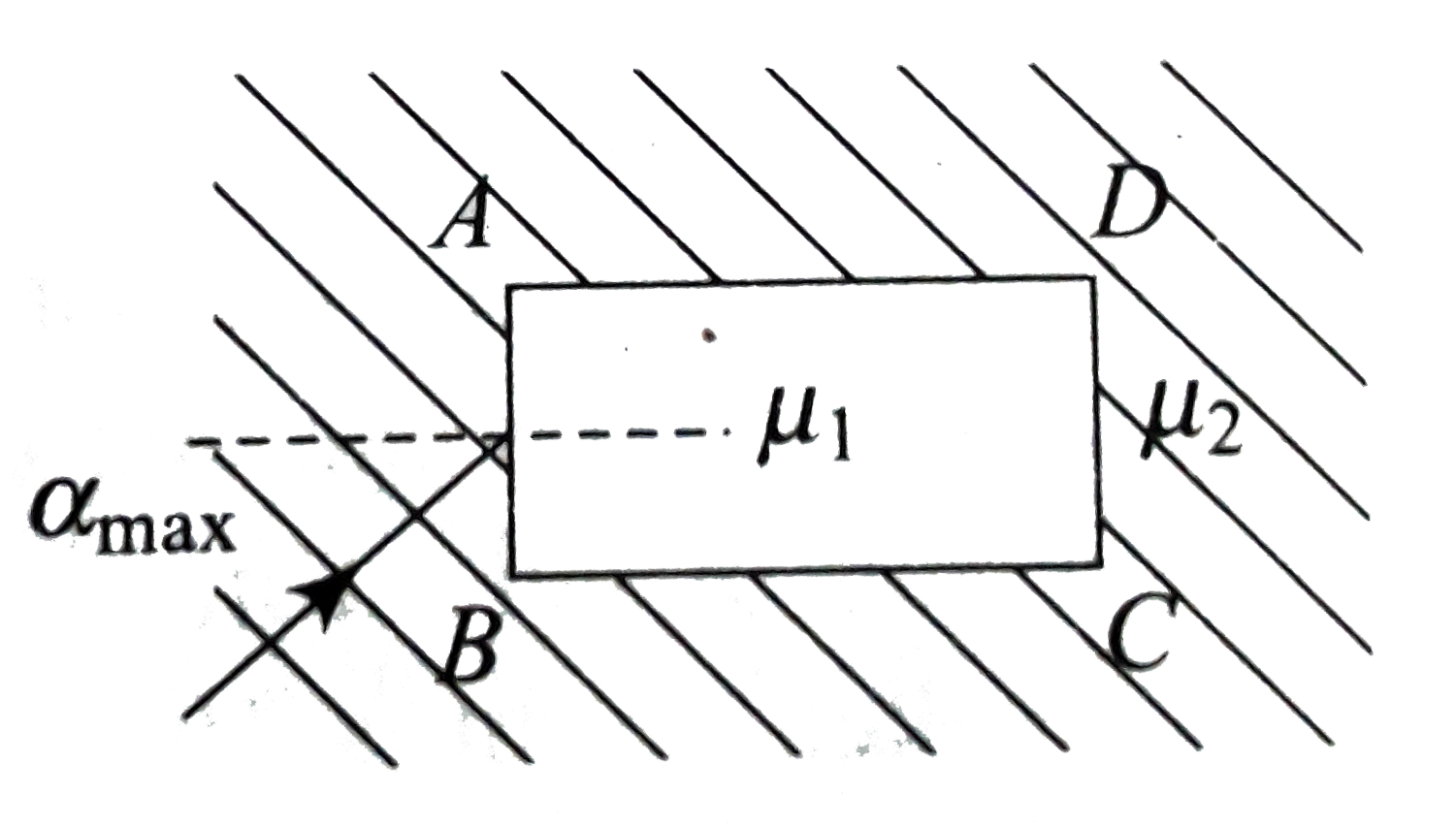 Asin−1[n1n2cos(sin−1(n2n1))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin−1(n2n1)
Asin−1[n1n2cos(sin−1(n2n1))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin−1(n2n1) - Question 3 - Select One
A rectengular glass slab ABCD of refractive index n_1 is immersed in water of refractive index n2(n1>n2). A ray of light is incident at the surface AB of the slab as shown. The maximum value of the angle of incidence αmax such that the ray comes out only from the other surface CD is given by
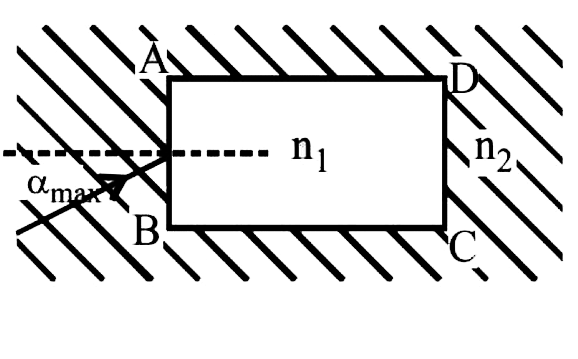 Asin−1[n1n2cos(sin−1(n2n2))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin^-1((n_2)/(n_2))
Asin−1[n1n2cos(sin−1(n2n2))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin^-1((n_2)/(n_2))
A ray of light is incident on the surface of a glass plate of index of refraction 1.55 at the polarizing angle. Calculate the angle of refraction.
View SolutionA ray is incident on a slab of refractive index 5/4 at an angle /θ as shown. Find maximum angle /θ so that TIR occur at surface AD.
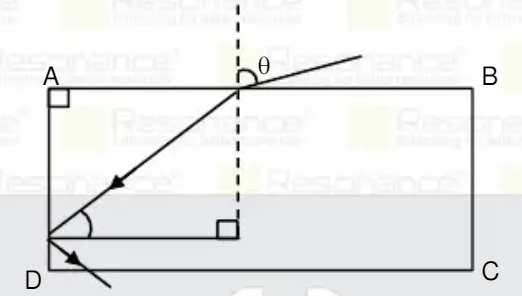 View Solution
View SolutionA transparent slab of thickness d has a refractive index n(z) that increases with z. Here z is the vertical distance inside the slab, measured from the top. The slab is placed between two media with uniform refractive indices n1andn2(>n1), as shown in the figure. A ray of light is incident with angle θi, from medium 1 and emerges in medium 2 with refraction and θf, with a lateral displacement l.
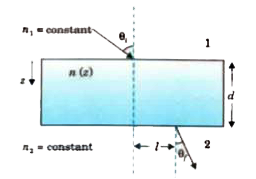
Which of the following statement(s) is (are) true ?View SolutionA ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle betweent the reflected and refracted rays is
View SolutionA ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle between the reflected and refracted rays is
View Solution
