A material is embedded between two glass plates. Refractive index n of the material varies with thickness as shown below. The maximum incident angle (in degrees) on the material for which beam will pass through the material is-
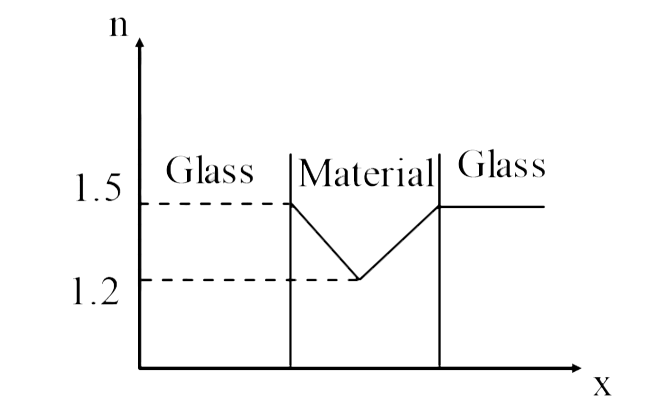
60
53.1
43.5
32.3
The correct Answer is:B
1.5×sini=1.2 sin r ⇒sin r =1.51.2sin i
TIR should not take place ∴sinr<1
1.51.2<sini<1
sini<1215⇒sini<0.8⇒sin45∘=1√2=0.707
⇒imax>45.
Similar Questions
Knowledge Check
The refractive index of material varies with wavelength according to the Cauchy’s relation is
Aμ=Aλ+BBμ=A+Bλ2Cμ=A×BλDμ=A2λ+BRefractive index of material is equal to tangent of polarising angle. It is called
ABrewster’s lawBLambert’s lawCMalus’s lawDBragg’s lawIf critical angle for a material to air is 30∘, the refractive index of the material will be
A1.0B1.5C2.0D2.5
A glass slab is made such that the refractive index of the material increases with its depth. The glass slab is kept in air and a light ray is incident on its top face. How will the light ray pass through it ?
View SolutionWhat is the refractive index of the material of the glass prism shown in the figure, if a ray of light incident normally at the face AB emerges along the face AC?
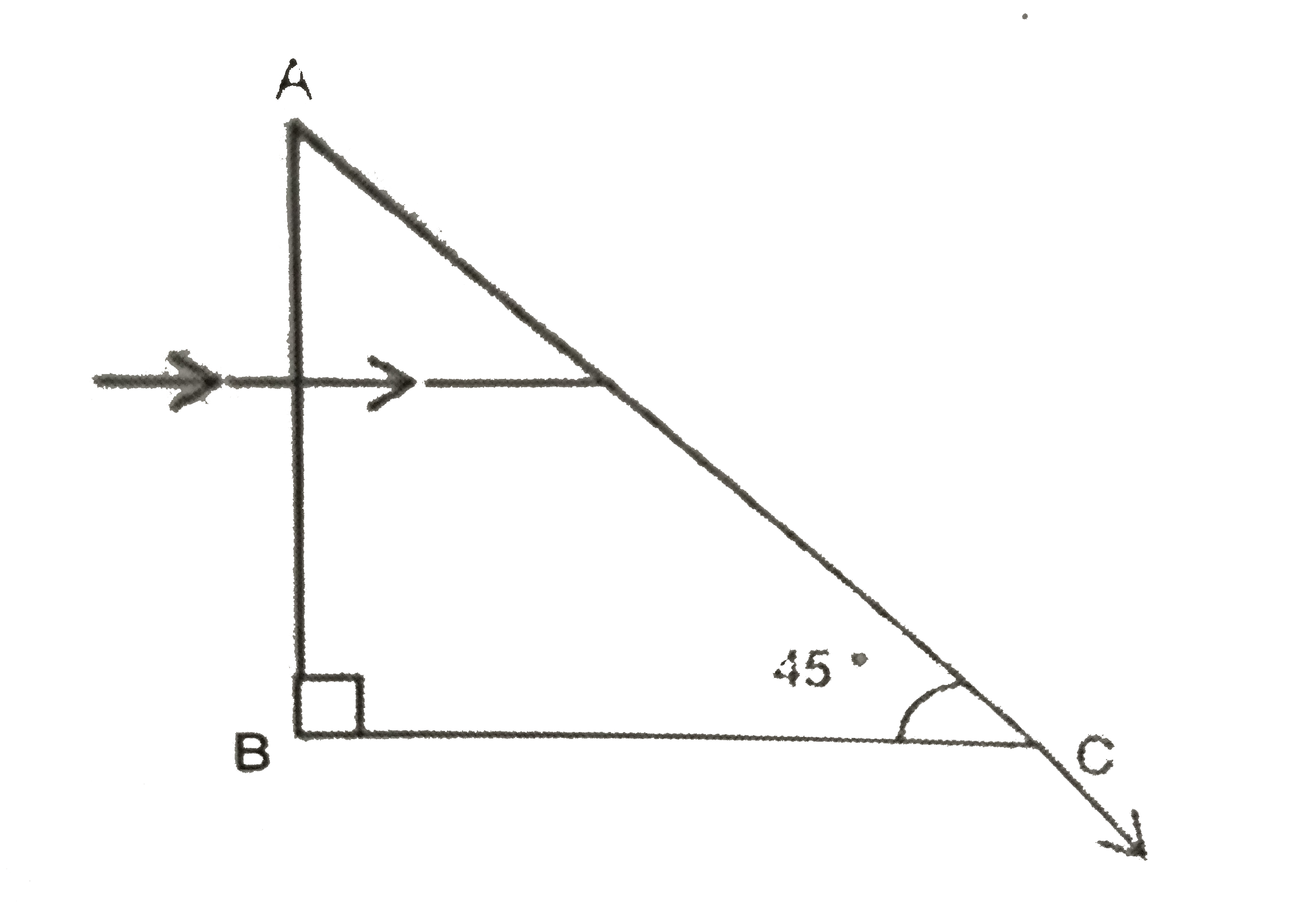
View SolutionThe refracting angle of the prism is 60∘ and the refractive index of the material of the prism is √3. Calculate the angle of minimum deviation in degree.
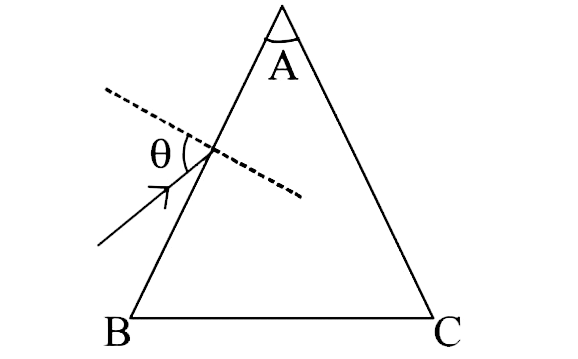
View SolutionMonochromatic light is incident on a glass prism of angle A. If the refractive index of the material of the prism is μ, a ray, incident at an angle θ, on the face AB would get transmitted through the face AC of the prism provided:
View SolutionThe refractive index of the material of a prism and liquid are 3/2 and 4/3 respectively. Critical angle C in glass can be expressed as
View Solution
