A ray of light is travelling from glass to air. (Refractive index of glass =1.5). The angle of incidence is 50∘. The deviation of the ray is
0∘
80∘
50∘− sin−1
sin−1[sin50∘1.5]−50∘
The correct Answer is:B
Critical angle
iC=sin−1(11.5)=42∘
Since, i>iC, so TIR will occur
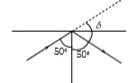
∴ δ=180∘−(50+50)=80∘ .
Similar Questions
Knowledge Check
A ray of light is travelling from glass to air. The angle of incidence in glass is 35∘, and angle of refraction in air 60∘. What is the refractive index of glass w.r.t. air ? [sin35∘=(0.5736)]
A1.9B0.5C1.51D2.0A ray of light passes from glass having a refractive index of 1.6, to air. The angle of incidence for which the angle of refraction is twice the angle of incidence is
Asin−1(45)Bsin−1(35)Csin−1(58)Dsin−1(25)A ray of light passes from glass, having a refractive indx of 1.6, to air. The angle of incidence for which the angle of refraction is twice the angle of incidence is
Asin−1(45)Bsin−1(35)Csin−1(58)Dsin−1(25)
A ray of light is incident on a glass plate of refractive index 1.5. The angle between the reflected and refracted rays is 90∘. What is the ratio of wavelenth of reflected to refracted rays?
View SolutionA ray of light travelling from glass to air is incident at 50∘ from the glass air boundary . What is the angle of deviation if the critical angle is 42∘ ?
View SolutionA ray of light travels from air to glass . It is found that the angle of refraction is half the angle of incidence . Then the angle of refraction is given by
View SolutionOne side of a glass slab is silvered as shown. A ray of light is incident on the other side at angle of incidence i=45∘ . Refractive index of glass is given as 1.5. The deviation of the ray of light from its initial path when it comes out of the slab is

View SolutionA ray of light enters a rectangular glass slab of refractive index √3 at an angle of incidence 60∘. It travels a distance of 5cm inside the slab and emerges out of the slab. The perpendicular distance between the incident and the emergent rays is
View Solution
