In a series circuit and , when the current in the circuit is maximum, at that time the ratio of the energies stored in the capacitor and the inductor will be
The correct Answer is:D
At resonance
Current is maximum
Energy stored in inductor
Energy stored in capacitor
Similar Questions
In an L−C circuit, L=0.75H and C=18μF, (a) At the instant when the current in the inductor is changing at a rate of 3.40Ns, what is the charge on the capacitor? (b) When the charge on the capacitor is 4.2×10−4 C, what is the induced emf in the inductor?
View SolutionIn the steady state of the circuit shown in the figure the ratio of energy stored in the inductor to th energy stored in the capacitor is 10000.
View Solution
Knowledge Check
In the circuit shown, the energy stored in 1μF capacitor is
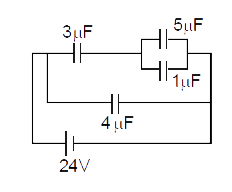A40μJB64μJC32μJDnone of theseA series RLC circuit is connected to an ac generator. The instant at which current in the circuit is zero, the energy stored in the capacitor and inductor are:
Azero in bothBmaximum in bothCzero & maximum respectivelyDmaximum & zero respectivelyA series LCR circuit has R=5Ω,L=40mH and C=1μF, the bandwidth of the circuit is
A10 HzB20 HzC30 HzD40 Hz
An L−C circuit consists of an inductor with L=0.0900H and a capacitor of C=4×10−4F. The initial charge on the capacitor is 5.00μC, and the initial current in the inductor is zero.
(a) What is the maximum voltage across the capacitor?
(b) What is the maximum current in the inductor?
(c) What is the maximum energy stored in the inductor?
(d) When the current in the inductor has half its maximum value, what is the charge on the capacitor and what is the energy stored in the inductor?
View SolutionA 1.00mH inductor and a 1.00μF capacitor are connected in series. The current in the circuit is described by i=20t, where t, is in second and i is in ampere. The capacitor initially has no charge. Determine
(a) the voltage across the inductor as a function of time,
(b) the voltage across the capacitor as a function of time,
(c) the time when the energy stored in the capacitor first exceeds that in the inductor.
View SolutionThe current in series LCR circuit will be the maximum when ω is
View SolutionIn an L−C circuit, L=3.3H and C=840pF. At t=0 charge on the capacitor is 105μC and maximum. Compute the following quantities at t=2.0ms.
a. The energy stored in the capacitor.
b. The total energy in the circuit,
c. The energy stored in the inductor.
View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View Solution